
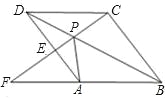
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线点F.问:
(1)图中△APD与哪个三角形全等?并说明理由;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
【答案】(1)△CPD.理由参见解析;(2)证明参见解析;(3)PC2=PEPF.理由参见解析.
【解析】
试题分析:(1)根据菱形的性质,利用SAS来判定两三角形全等;(2)根据第一问的全等三角形结论及已知,利用两组角相等则两三角形相似来判定即可;(3)根据相似三角形的对应边成比例及全等三角形的对应边相等即可得到结论.
试题解析:(1)△APD≌△CPD.理由:∵四边形ABCD是菱形,∴AD=CD,∠ADP=∠CDP.又∵PD=PD,∴△APD≌△CPD(SAS).(2)∵△APD≌△CPD,∴∠DAP=∠DCP,∵CD∥AB,∴∠DCF=∠DAP=∠CFB,又∵∠FPA=∠FPA,∴△APE∽△FPA(两组角相等则两三角形相似).(3)猜想:PC2=PEPF.理由:∵△APE∽△FPA,∴![]() .即PA2=PEPF.∵△APD≌△CPD,∴PA=PC.∴PC2=PEPF.
.即PA2=PEPF.∵△APD≌△CPD,∴PA=PC.∴PC2=PEPF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】口袋内装有除颜色外完全相同的红球、白球和黑球共10个,从中摸出一球,摸出红球的概率是0.2,摸出白球的概率是0.5,那么黑球的个数是_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
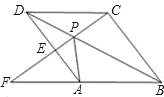
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农户去年承包荒山若干亩,投资7800 元改造后,种果树2000棵.今年水果总产量为18000千克,此水果在市场上每千克售a元,在果园每千克售b元(b<a).该农户将水果拉到市场出售平均每天出售1000千克,需8 人帮忙,每人每天付工资25元,农用车运费及其他各项税费平均每天100元.
(1)分别用a,b表示两种方式出售水果的收入?
(2)若a=1.3元,b=1.1元,且两种出售水果方式都在相同的时间内售完全部水果,请你通过计算说明选择哪种出售方式较好.
(3)该农户加强果园管理,力争到明年纯收入达到15000元,那么纯收入增长率是多少?(纯收入=总收入﹣总支出,该农户采用了(2)中较好的出售方式出售)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现实生活中,如果收入1000元记作+1000元,那么﹣800表示( )
A. 支出800元 B. 收入800元 C. 支出200元 D. 收入200元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABD和△ACE中,有下列判断:
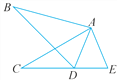
①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.
请用其中的三个判断作为条件,余下的一个判断作为结论(用序号的形式),写出一个由三个条件能推出结论成立的式子,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com