
【题目】如图,在△ABD和△ACE中,有下列判断:
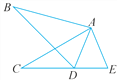
①AB=AC;②∠B=∠C;③∠BAC=∠EAD;④AD=AE.
请用其中的三个判断作为条件,余下的一个判断作为结论(用序号的形式),写出一个由三个条件能推出结论成立的式子,并说明理由.
【答案】证明见解析
【解析】试题分析:
按题中要求,选3个作条件,1个作结论,则有:(1)① ② ③ ④ ;(2)①②④③;(3)①③④②;(4)②③④①;共计四种组合方式.然后根据全等三角形的判定方法,可知其中(2)不能判定△ABD≌△ACE,从而不能得到结论,其余的三种组合都可以通过证△ABD≌△ACE而得到结论,故有三种组合方式是成立的,我们选择其中一个进行证明即可.
试题解析:
(1)有三种组合是成立的:① ② ③④ 或①③④② 或②③④①.
(2)如①②③④ 理由如下:
∵∠BAC=∠EAD,
∴∠BAC+∠CAD=∠EAD+∠CAD,即∠BAD=∠CAE,
∴在△ABD和△ACE中: 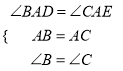 ,
,
∴△ABD≌△ACE(ASA).
∴ AD=AE.


科目:初中数学 来源: 题型:
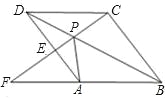
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线点F.问:
(1)图中△APD与哪个三角形全等?并说明理由;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE,PF之间存在什么关系?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是BC边上一点,AB⊥BC于点B,DC⊥BC于点C,AB=BC,∠A=∠CBD,AE与BD交于点O,有下列结论:①AE=BD;②AE⊥BD;③BE=CD;④△AOB的面积等于四边形CDOE的面积.其中正确的结论有( )
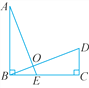
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是甲、乙两人同一地点出发后,路程随时间变化的图象.

(1)两个变量中, 是自变量, 是因变量;
(2)甲的速度 乙的速度(填<、=、或>);
(3)路程为150km时,甲行驶了 小时,乙行驶了 小时.
(4)甲比乙先走了 小时;在9时, 走在前面。
查看答案和解析>>
科目:初中数学 来源: 题型:
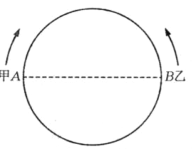
【题目】某校为培养青少年科技创新能力,举办了动漫制作活动,小明设计了点做圆周运动的一个雏型.如图所示,甲、乙两点分别从直径的两端点 A、B以顺时针、逆时针的方向同时沿圆周运动. 甲运动的路程l(cm)与时间t(s)满足关系:![]() (t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为 21 cm.
(t≥0),乙以4 cm/s的速度匀速运动,半圆的长度为 21 cm.
(1)甲运动 4 s后的路程是多少?
(2)甲、乙从开始运动到第一次相遇时,它们运动了多少时间?
(3)甲、乙从开始运动到第二次相遇时,它们运动了多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)交x轴于A(﹣1,0),B(5,0)两点,与y轴交于点C(0,2)
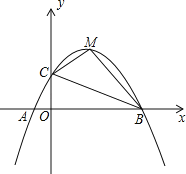
(1)求抛物线的解析式;
(2)若点M为抛物线的顶点,连接BC、CM、BM,求△BCM的面积;
(3)连接AC,在x轴上是否存在点P使△ACP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】七年级(2)班派出12名同学参加数学竞赛,老师以75分为基准,把分数超过75分的部分记为正数,不足的部分记为负数.评分记录如下:
+15,+20,-5,-4,-3,+4,+6,+2,+3,+5,+7,-8
(1)这12名同学中最高分和最低分各是多少分?
(2)超过基准分的有多少人?
(3)这12名同学的平均成绩是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com