
【题目】如图是一块残缺的圆轮片,点A、B、C在圆弧E上.
(1)画出![]() 所在的⊙O;
所在的⊙O;
(2)若AB=BC=60,∠ABC=120°,求![]() 所在⊙O的半径.
所在⊙O的半径.
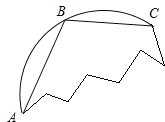
【答案】(1)作图参见解析;(2)60.
【解析】
试题分析:(1)先找到圆心,利用尺规作图,作出线段AB和BC的垂直平分线,两垂直平分线的交点即为圆心O,以O为圆心,OA或OB或OC长为半径画圆,即为弧AC所在的圆O;(2)利用边边边判定三角形ABO和三角形BOC全等,从而算出∠CBO=60度,然后能判断出三角形BOC是等边三角形,进而求出圆O的半径.
试题解析:(1)如图所示:先找到圆心,利用尺规作图,作出线段AB和BC的垂直平分线,两垂直平分线的交点即为圆心O,以O为圆心,OA长为半径画圆,即为弧AC所在的圆O;
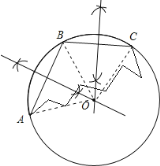 (2)如图,连接OA、OB、OC,∵AB=BC,AO=BO=CO, ∴△AOB≌△BOC,∠BAO=∠ABO=∠CBO=∠BCO, ∵∠ABC=120°,∴∠CBO=∠ABO=60°,∵BO=CO,∴∠OBC=∠BCO=60°,∴△OBC是等边三角形,∵BC=60,∴半径为60.
(2)如图,连接OA、OB、OC,∵AB=BC,AO=BO=CO, ∴△AOB≌△BOC,∠BAO=∠ABO=∠CBO=∠BCO, ∵∠ABC=120°,∴∠CBO=∠ABO=60°,∵BO=CO,∴∠OBC=∠BCO=60°,∴△OBC是等边三角形,∵BC=60,∴半径为60.


科目:初中数学 来源: 题型:
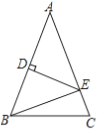
【题目】如图,△ABC中,AB=AC,AB的垂直平分线交边AB于D点,交边AC于E点,若△ABC与△EBC的周长分别是40cm,24cm,则AB=________cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个材质均匀的正方体的每个面上标有数字1,2,3中的其中一个,其展开图如图所示,随机抛掷此正方体一次,则朝上与朝下的两面上数字相同的概率是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在8×8的网格中,我们把△ABC在图1中作轴对称变换,在图2中作旋转变换,已知网格中的线段ED、线段MN分别是边AB经两种不同变换后所得的像,请在两图中分别画出△ABC经各自变换后的像,并标出对称轴和旋转中心(要求:不写作法,作图工具不限,但要保留作图痕迹).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中:
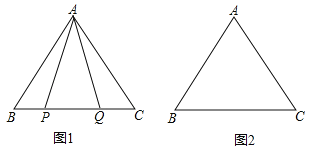
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com