
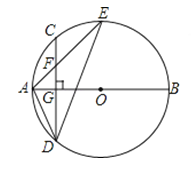
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;
;
④S△DEF=![]() .其中正确的是结论的个数是( )
.其中正确的是结论的个数是( )
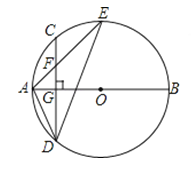
(A)1 (B)2 (C)3 (D)4
【答案】C
【解析】分析:①由垂径定理证得∠ADF=∠AED;②由垂径定理证得DG=CG;③∠E=∠ADG,在Rt△ADG中,求tan∠ADG;④先S△ADF,由△AFD∽△ADE,求得S△ADE;
详解:①∵AB是⊙O的直径,弦CD⊥AB,∴DG=CG,
∴弧AD=弧AC,∠ADF=∠AED,
∵∠FAD=∠DAE,∴△ADF∽△AED;
②∵![]() ,CF=2,∴FD=6,
,CF=2,∴FD=6,
∴CD=DF+CF=8,∴CG=DG=4,
∴FG=CG-CF=2;
③Rt△AFG中,AF=3,FG=2,由勾股定理得AG=![]() ,
,
Rt△ADG中,tan∠ADG=![]() .
.
∵∠E=∠ADG,所以tanE![]() .
.
④Rt△ADG中,AG=![]() ,DG=4,由勾股定理得AD=
,DG=4,由勾股定理得AD=![]() ,
,
S△ADF=![]() DF·AG=
DF·AG=![]() ×6×
×6×![]() .
.
∵∠ADF=∠E,∠DAF=∠EAD,∴△AFD∽△ADE,
∴![]() ,即
,即![]() ,则S△ADE=
,则S△ADE=![]() .
.
∵S△DEF=S△ADE-S△AFD,∴S△DEF=![]() ,
,
所以正确的结论是①②④.
故选C.


 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
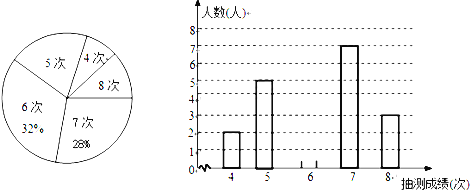
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2
(1)在直线l上任取两点A,B;
(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;
(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是_________________________________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() (m>0)与x轴的交点为A,B.
(m>0)与x轴的交点为A,B.
(1)求抛物线的顶点坐标;
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求线段AB上整点的个数;
②若抛物线在点A,B之间的部分与线段AB所围成的区域内(包括边界)恰有6个整点,结合函数的图象,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为16, G、H分别为AB. AC的中点,分别以AB.AC为斜边向外作Rt△ADB和Rt△AEC,连接DG.GH,EH,则DG+GH+EH的值为__________.
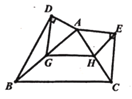
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标中,边长为1的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转.旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图1).
(1)求边AB在旋转过程中所扫过的面积;
(2)设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论;
(3)设MN=m,当m为何值时△OMN的面积最小,最小值是多少?并直接写出此时△BMN内切圆的半径.
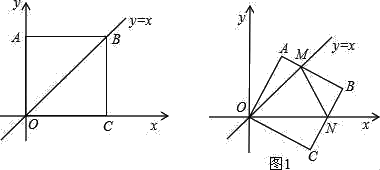
查看答案和解析>>
科目:初中数学 来源: 题型:
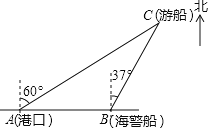
【题目】一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,
(1)求点C到直线AB的距离;
(2)求海警船到达事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=2![]() ,AD=6,P为边AD上一点,且AP=2,在对角线BD上寻找一点M,使AM+PM最小,则AM+PM的最小值为_____.
,AD=6,P为边AD上一点,且AP=2,在对角线BD上寻找一点M,使AM+PM最小,则AM+PM的最小值为_____.
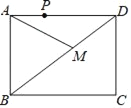
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,某市制定了如下用水收费标准:每户每月的用水不超过10吨时,水价为每吨1.2元;超过10吨时,超过部分按每吨1.8元收费,该市某户居民5月份用水![]() 吨
吨![]() ,应缴水费
,应缴水费![]() 元.
元.
(1)写出![]() 与
与![]() 之间的关系式;
之间的关系式;
(2)某户居民若5月份用水16吨,应缴水费多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com