
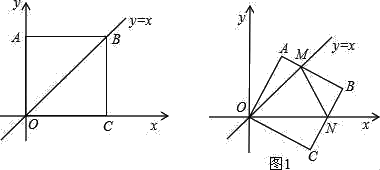
【题目】在平面直角坐标中,边长为1的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转.旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图1).
(1)求边AB在旋转过程中所扫过的面积;
(2)设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论;
(3)设MN=m,当m为何值时△OMN的面积最小,最小值是多少?并直接写出此时△BMN内切圆的半径.
【答案】(1)![]() ;(2)无变化;(3)
;(2)无变化;(3)![]() ,
,![]() ,
,![]()
【解析】分析:(1)阴影部分不是一个规则图形,它的面积等于S阴=S△OAB+S扇形OBB′﹣S△OA'B′﹣S扇形OAA′=S扇形OBB′﹣S扇形OAA′;(2)证明△OAE≌△OCN(AAS),△OME≌△OMN(SAS),得到p=MN+BN+BM=AB+BC;(3)S△MON=S△MOE=![]() OA×EM=
OA×EM=![]() m,即是要求m的最小值,设AM=n,在Rt△BMN中,由勾股定理得到关于n的一元二次方程,根据△≥求m的最小值,直角三角形的内切圆的半径等于直角边的和与斜边差的一半.
m,即是要求m的最小值,设AM=n,在Rt△BMN中,由勾股定理得到关于n的一元二次方程,根据△≥求m的最小值,直角三角形的内切圆的半径等于直角边的和与斜边差的一半.
详解:解:(1)如图,S阴=S△OAB+S扇形OBB′﹣S△OA′B′﹣S扇形OAA′
=S扇形OBB′﹣S扇形OAA′=![]() ﹣
﹣![]() .
.
(2)p值无变化
证明:延长BA交y轴于E点,
在△OAE与△OCN中,
∠AOE=∠CON=90°-∠AON,∠OAE=∠OCN=90°,OA=OC,
∴△OAE≌△OCN(AAS),∴OE=ON,AE=CN.
在△OME与△OMN中,
OE=ON,∠MOE=∠MON=45°,OM=OM,
∴△OME≌△OMN(SAS),∴MN=ME=AM+AE=AM+CN,
∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=2;
(3)设AM=n,则BM=1﹣n,CN=m﹣n,BN=1﹣m+n,
∵△OME≌△OMN,∴S△MON=S△MOE=![]() OA×EM=
OA×EM=![]() m,
m,
在Rt△BMN中,BM2+BN2=MN2,
∴(1﹣n)2+(1﹣m+n)2=m2,化简得,n2﹣mn+1﹣m=0
∴△=m2﹣4(1﹣m)≥0,解得,m≥![]() ﹣2或m≤﹣
﹣2或m≤﹣![]() ﹣2,
﹣2,
∴当m=![]() ﹣2时,△OMN的面积最小为
﹣2时,△OMN的面积最小为![]() ﹣1.
﹣1.
此时n=![]() ﹣1,
﹣1,
则BM=1﹣n=2﹣![]() ,BN=1﹣m+n=2﹣
,BN=1﹣m+n=2﹣![]() ,
,
∴Rt△BMN的内切圆半径为![]() =3﹣
=3﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.
![]() 过点C画线段AB的平行线CD;
过点C画线段AB的平行线CD;
![]() 过点A画线段BC的垂线,垂足为E;
过点A画线段BC的垂线,垂足为E;
![]() 过点A画线段AB的垂线,交线段CB的延长线于点F;
过点A画线段AB的垂线,交线段CB的延长线于点F;
![]() 线段AE的长度是点______到直线______的距离;
线段AE的长度是点______到直线______的距离;
![]() 线段AE、BF、AF的大小关系是______
线段AE、BF、AF的大小关系是______![]() 用“
用“![]() ”连接
”连接![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】调查作业:了解你所住小区家庭5月份用气量情况.
小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2-5之间,这300户家庭的平均人数均为3.4.
小天、小东、小芸各自对该小区家庭5月份用气量情况进行了抽样调查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
表1 抽样调查小区4户家庭5月份用气量统计表 (单位:![]() )
)

表2 抽样调查小区15户家庭5月份用气量统计表 (单位:![]() )
)

表3 抽样调查小区15户家庭5月份用气量统计表 (单位:![]() )
)

根据以上材料回答问题:
小天、小东和小芸三人中,哪一位同学抽样调查的数据能较好地反映出该小区家庭5月份用气量情况,并简要说明其他两位同学抽样调查地不足之处.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中有“盈不足术”的问题,原文如下:“今有共买羊,人出五,不足四十五;人出七,不足三.问人数、羊价各几何?”题意是:若干人共同出资买羊,每人出![]() 文,则差
文,则差![]() 文;每人出
文;每人出![]() 文,则差
文,则差![]() 文.
文.
(1)设人数为![]() ,则用含
,则用含![]() 的代数式表示羊价为___________或___________;
的代数式表示羊价为___________或___________;
(2)求人数和羊价各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() ,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=
,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=![]() ;
;
④S△DEF=![]() .其中正确的是结论的个数是( )
.其中正确的是结论的个数是( )
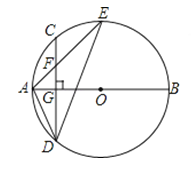
(A)1 (B)2 (C)3 (D)4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上的口令:立正,向右转,向后转,向左转之间可以相加.连结执行两个口令就把这两个口令加起来.例如:向右转+向左转=立正;向左转+向后转=向右转.如果分别用0,1,2,3分别代表立正,向右转,向后转,向左转,就可以用如图所示的加法表来表示,在表中填了部分的数值和代表数值的字母.下列对于字母![]() 的值,说法错误的是( )
的值,说法错误的是( )
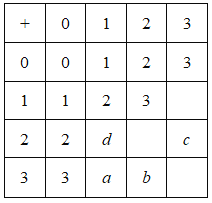
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
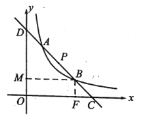
【题目】已知直线l过点P(2, 2),且与函数y=![]() (x>0)的图象相交于A, B两点,与x轴、y轴分别交于点C, D,如图所示,四边形OFBM为矩形,面积为3.
(x>0)的图象相交于A, B两点,与x轴、y轴分别交于点C, D,如图所示,四边形OFBM为矩形,面积为3.
(1)求k的值;
(2)当点B的横坐标为3时,求直线l的解析式及线段BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一节数学活动课上,王老师将本班学生身高数据(精确到1厘米)出示给大家,要求同学们各自独立绘制一幅频数分布直方图,甲绘制的如图①所示,乙绘制的如图②所示,经王老师批改,甲绘制的图是正确的,乙在数据整理与绘图过程中均有个别错误.
(1)写出乙同学在数据整理或绘图过程中的错误(写出一个即可);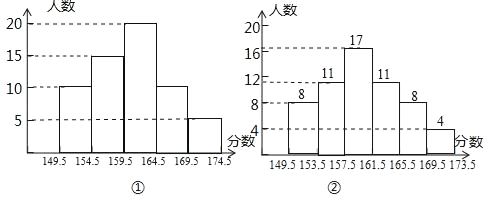
(2)甲同学在数据整理后若用扇形统计图表示,则159.5﹣164.5这一部分所对应的扇形圆心角的度数为 ;
(3)该班学生的身高数据的中位数是 ;
(4)假设身高在169.5﹣174.5范围的5名同学中,有2名女同学,班主任老师想在这5名同学中选出2名同学作为本班的正、副旗手,那么恰好选中一名男同学和一名女同学当正,副旗手的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,约定:上方相邻两数之和等于这两数下方箭头共同指向的数.
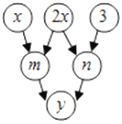
示例: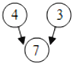 即
即![]()
则(1)用含![]() 的式子表示
的式子表示![]() ______;
______;
(2)当![]() 时,
时,![]() ______,
______,![]() 的值为______.
的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com