
【题目】在学校科技周活动中,丛明和蔡智同学制作的智能小车![]() ,
,![]() 做圆周(等分为
做圆周(等分为![]() 格)运动,规定顺时针方向为负运动,逆时针方向为正运动.若两小车
格)运动,规定顺时针方向为负运动,逆时针方向为正运动.若两小车![]() ,
,![]() 从
从![]() 点同时出发,当它们按
点同时出发,当它们按![]() 的速度运动到
的速度运动到![]() 秒时,共行
秒时,共行![]() 格.
格.
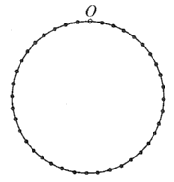
(1)求两小车的运动速度;若![]() 作正运动,
作正运动,![]() 作负运动,标出小车运动到
作负运动,标出小车运动到![]() 秒时的位置
秒时的位置![]() ,
,![]() ;
;
(2)若![]() ,
,![]() 从(1)中的位置同时出发,都沿正方向运动,再经多久时
从(1)中的位置同时出发,都沿正方向运动,再经多久时![]() ,
,![]() 所到达位置表示的数互为相反数?
所到达位置表示的数互为相反数?
(3)若![]() ,
,![]() 从(2)中的位置同时出发相向运动,当它们在
从(2)中的位置同时出发相向运动,当它们在![]() 点相遇时,
点相遇时,![]() 点所对应的数是多少?
点所对应的数是多少?
(4)若![]() ,
,![]() 从(3)中的位置同时出发,都沿负方向运动,经过多长时间
从(3)中的位置同时出发,都沿负方向运动,经过多长时间![]() ,
,![]() 首次相遇?
首次相遇?
【答案】(1)见解析;(2)再经过![]() 秒
秒![]() ,
,![]() 表示的数互为相反数;(3)1.5;(4)经过
表示的数互为相反数;(3)1.5;(4)经过![]() 秒后
秒后![]() ,
,![]() 两小车首次相遇
两小车首次相遇
【解析】
(1)先求出![]() ,
,![]() 的速度之和,由A、
的速度之和,由A、![]() 的速度比是
的速度比是![]() 求得A、B的速度,再由运动路程=速度
求得A、B的速度,再由运动路程=速度![]() 时间以及
时间以及![]() 作正运动,
作正运动,![]() 作负运动,标出小车运动到
作负运动,标出小车运动到![]() 秒时的位置
秒时的位置![]() ,
,![]() 即可;
即可;
(2)设再经过![]() 秒
秒![]() ,
,![]() 所到达位置表示的数互为相反数,据此列一元一次方程,解之即可;
所到达位置表示的数互为相反数,据此列一元一次方程,解之即可;
(3)由(2)知![]() ,
,![]() 之间的距离为
之间的距离为![]() .设经过
.设经过![]() 秒
秒![]() ,
,![]() 在
在![]() 点相遇,据此列一元一次方程,解之即可;
点相遇,据此列一元一次方程,解之即可;
(4)设经过![]() 秒
秒![]() ,
,![]() 两小车首次相遇,据此列一元一次方程,解之即可.
两小车首次相遇,据此列一元一次方程,解之即可.
(1)根据题意得![]() ,
,![]() 的速度和为
的速度和为![]() (格/秒)
(格/秒)
![]() ,
,![]() 的速度比是
的速度比是![]() ,
,
![]() 的速度是
的速度是![]() (格/秒),A的运动路程=1
(格/秒),A的运动路程=1![]() 2=2(格)
2=2(格)
![]() 的速度是
的速度是![]() (格/秒),B的运动路程=3
(格/秒),B的运动路程=3![]() 2=6(格)
2=6(格)
如图,

(2)
如图:
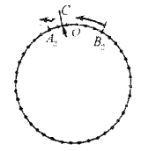
设再经过![]() 秒
秒![]() ,
,![]() 所到达位置表示的数互为相反数,
所到达位置表示的数互为相反数,
则![]() .
.
解得![]() .
.
答:再经过![]() 秒
秒![]() ,
,![]() 表示的数互为相反数.
表示的数互为相反数.
(3)由(2)知![]() ,
,![]() 所到达位置表示的数分别为
所到达位置表示的数分别为![]() 和
和![]() ,它们之间的距离为
,它们之间的距离为![]() ,
,
设经过![]() 秒
秒![]() ,
,![]() 在
在![]() 点相遇,
点相遇,
则![]() ,
,
解得![]() ,
,
![]() 点所对应的数为
点所对应的数为![]() .
.
(4)如图:

设经过![]() 秒
秒![]() ,
,![]() 两小车首次相遇,
两小车首次相遇,
则![]() .
.
解得![]() .
.
答:经过![]() 秒后
秒后![]() ,
,![]() 两小车首次相遇.
两小车首次相遇.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,D是BC边上一点,将△ABD绕点A逆时针旋转60°得到△ACE,连接DE,则下列说法不一定正确的是( )
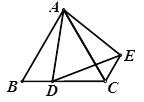
A. △ADE是等边三角形 B. AB∥CE C. ∠BAD=∠DEC D. AC=CD+CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我区的数学爱好者申请了一项省级课题——《中学学科核心素养理念下渗透数学美育的研究》,为了了解学生对数学美的了解情况,随机抽取部分学生进行问卷调查,按照“理解、了解、不太了解、不知道”四个类型,课题组绘制了如下两幅不完整的统计图,请根据统计图中提供的信息,回答下列问题:
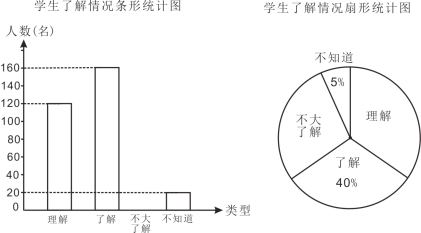
(1)本次调查共抽取了多少名学生?并补全条形统计图;
(2)在扇形统计图中,“理解”所占扇形的圆心角是多少度?
(3)我区七年级大约8000名学生,请估计“理解”和“了解”的共有学生多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保证达万高速公路在2012年底全线顺利通车,某路段规定在若干天内完成修建任务.已知甲队单独完成这项工程比规定时间多用10天,乙队单独完成这项工程比规定时间多用40天,如果甲、乙两队合作,可比规定时间提前14天完成任务.若设规定的时间为x天,由题意列出的方程是( )
A.![]() +
+![]() =
=![]() B.
B.![]() +
+![]() =
=![]()
C.![]() -
-![]() =
=![]() D.
D.![]() +
+![]() =
=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面4个说法中,正确的个数为( ).
(1)“从袋中取出一只红球的概率是99%”,这句话的意思是肯定会取出一只红球,因为概率已经很大
(2)袋中有红、黄、白三种颜色的小球,这些小球除颜色外没有其他差别,因为小张对取出一只红球没有把握,所以小张说:“从袋中取出一只红球的概率是50%”
(3)小李说,这次考试我得90分以上的概率是200%
(4)“从盒中取出一只红球的概率是0”,这句话是说取出一只红球的可能性很小
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在直角梯形ABCD中, AD∥BC,∠BCD=90°, BC=CD=2AD , E、F分别是BC、CD边的中点,连结BF、DE交于点P,连结CP并延长交AB于点Q,连结AF,则下列结论不正确的是( )
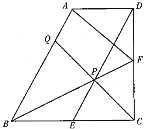
A.CP 平分∠BCDB.四边形 ABED 为平行四边形
C.CQ将直角梯形 ABCD 分为面积相等的两部分D.△ABF为等腰三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD内的任意一点,连接PA、PB、PC、PD,得到△PAB、△PBC、△PCD、△PDA,设它们的面积分别是S1、S2、S3、S4,给出如下结论:
①S1+S2=S3+S4② S2+S4= S1+ S3
③若S3=2S1,则S4=2S2④若S1= S2,则P点在矩形的对角线上
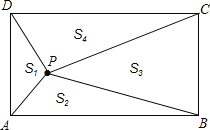
其中正确的结论的序号是 ▲ (把所有正确结论的序号都填在横线上).
查看答案和解析>>
科目:初中数学 来源: 题型:
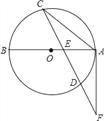
【题目】如图,已知AB是⊙O的直径,弦CD与AB交于点E,F为CD的延长线上一点,连接AF,且FA2=FDFC.
(1)求证:FA为⊙O的切线;
(2)若AC=8,CE:ED=6:5,AE:EB=2:3,求AB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南昌的雾霾引起了小张对环保问题的重视.一次旅游小张思考了一个问题.从某地到南昌,若乘火车需要![]() 小时,若乘汽车需要
小时,若乘汽车需要![]() 小时.这两种交通工具平均每小时二氧化碳的排放量之和为
小时.这两种交通工具平均每小时二氧化碳的排放量之和为![]() 千克,火车全程二氧化碳的排放总量比汽车的多
千克,火车全程二氧化碳的排放总量比汽车的多![]() 千克,分别求火车和汽车平均每小时二氧化碳的排放量.
千克,分别求火车和汽车平均每小时二氧化碳的排放量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com