
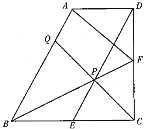
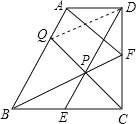
【题目】已知在直角梯形ABCD中, AD∥BC,∠BCD=90°, BC=CD=2AD , E、F分别是BC、CD边的中点,连结BF、DE交于点P,连结CP并延长交AB于点Q,连结AF,则下列结论不正确的是( )
A.CP 平分∠BCDB.四边形 ABED 为平行四边形
C.CQ将直角梯形 ABCD 分为面积相等的两部分D.△ABF为等腰三角形
【答案】C
【解析】
A.根据边角边”证明△BCF≌△DCE,然后利用“角边角”证明△BEP≌△DFP,再利用“边角边”证明△BCP≌△DCP全等,根据全等三角形对应角相等可得∠BCP=∠DCP;
B.根据一组对边平行且相等的四边形是平行四边形可得四边形ABED为平行四边形;
C. 连接QD,利用“边角边”证明△BCQ和△DCQ全等,根据全等三角形的面积相等判断出S△BCQ=S△DCQ,判断出CQ将直角梯形ABCD分成的两部分面积不相等.
D. 根据平行四边形的对边相等可得AB=DE,再求出AB=BF,从而得到△ABF为等腰三角形;
解:∵BC=CD,E、F分别是BC、CD边的中点,
∴BE=CE=CF=DF,
在△BCF和△DCE中,
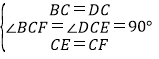 ,
,
∴△BCF≌△DCE(SAS),
∴DE=BF,∠CBF=∠CDE,∠BFC=∠DEC,
∴180°-∠BFC=180°-∠DEC,
即∠BEP=∠DFP,
在△BEP和△DFP中,
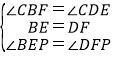 ,
,
∴△BEP≌△DFP(ASA),
∴BP=DP,
在△BCP和△DCP中,
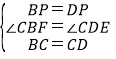 ,
,
∴△BCP≌△DCP(SAS),
∴∠BCP=∠DCP,
∴CP平分∠BCD,故A选项结论正确;
∵BC=2AD,E是BC的中点,
∴BE=AD,
又∵AD∥BC,
∴四边形ABED为平行四边形,故B选项结论正确;
∴AB=DE,
又∵DE=BF(已证),
∴AE=BF,
∴△ABF为等腰三角形,故D选项结论正确;
连接QD,
在△BCQ和△DCQ中,
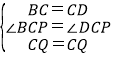 ,
,
∴△BCQ≌△DCQ(SAS),
∴S△BCQ=S△DCQ,
∴CQ将直角梯形ABCD分成的两部分面积不相等,故C选项结论不正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,是一张平行四边形纸片ABCD,要求利用所学知识作出一个菱形,甲、乙两位同学的作法分别如下:
甲:连接AC,作AC的中垂线交AD、BC于E、F,则四边形AFCE是菱形. | 乙:分别作 |
对于甲、乙两人的作法,可判断( )

A.甲正确,乙错误B.甲错误,乙正确
C.甲、乙均正确D.甲、乙均错误
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋中装有相同的三个小球,其上面分别标注
数字1、2、3、,现从中任意摸出一个小球,将其上面的数字作为点M的横坐标;将球放回
袋中搅匀,再从中任意摸出一个小球,将其上面的数字作为点M的纵坐标.
(1)写出点M坐标的所有可能的结果;
(2)求点M在直线y=x上的概率;
(3)求点M的横坐标与纵坐标之和是偶数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两人加工同一种零件,每小时甲比乙多加工10个这种零件,甲加工150个这种零件所用的时间与乙加工120个这种零件所用的时间相等,
(1)甲、乙两人每小时各加工多少个这种零件?
(2)该工厂计划加工920个零件,甲参与加工这批零件不超过12天,则乙至少加工多少天才能加工完这批零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学校科技周活动中,丛明和蔡智同学制作的智能小车![]() ,
,![]() 做圆周(等分为
做圆周(等分为![]() 格)运动,规定顺时针方向为负运动,逆时针方向为正运动.若两小车
格)运动,规定顺时针方向为负运动,逆时针方向为正运动.若两小车![]() ,
,![]() 从
从![]() 点同时出发,当它们按
点同时出发,当它们按![]() 的速度运动到
的速度运动到![]() 秒时,共行
秒时,共行![]() 格.
格.
(1)求两小车的运动速度;若![]() 作正运动,
作正运动,![]() 作负运动,标出小车运动到
作负运动,标出小车运动到![]() 秒时的位置
秒时的位置![]() ,
,![]() ;
;
(2)若![]() ,
,![]() 从(1)中的位置同时出发,都沿正方向运动,再经多久时
从(1)中的位置同时出发,都沿正方向运动,再经多久时![]() ,
,![]() 所到达位置表示的数互为相反数?
所到达位置表示的数互为相反数?
(3)若![]() ,
,![]() 从(2)中的位置同时出发相向运动,当它们在
从(2)中的位置同时出发相向运动,当它们在![]() 点相遇时,
点相遇时,![]() 点所对应的数是多少?
点所对应的数是多少?
(4)若![]() ,
,![]() 从(3)中的位置同时出发,都沿负方向运动,经过多长时间
从(3)中的位置同时出发,都沿负方向运动,经过多长时间![]() ,
,![]() 首次相遇?
首次相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
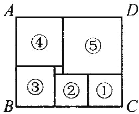
【题目】如图所示,是一块电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,则这个矩形的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
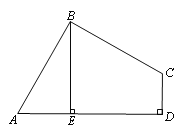
【题目】已知:如图,在四边形ABCD中,∠ABC=90°,CD⊥AD,AD2+CD2=2AB2.
(1)求证:AB=BC;
(2)当BE⊥AD于E时,试证明:BE=AE+CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
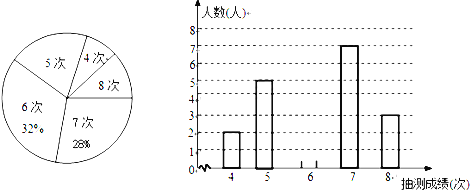
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“经过已知直线外一点作这条直线的垂线”的尺规作图过程:
已知:直线l和l外一点P.(如图1)
求作:直线l的垂线,使它经过点P.
作法:如图2
(1)在直线l上任取两点A,B;
(2)分别以点A,B为圆心,AP,BP长为半径作弧,两弧相交于点Q;
(3)作直线PQ.
所以直线PQ就是所求的垂线.
请回答:该作图的依据是_________________________________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com