
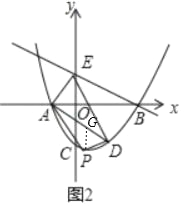
����Ŀ����ͼ1��������y=ax2+bx��2��x�ύ�ڵ�A����1��0����B��4��0�����㣬��y�ύ�ڵ�C��������B��ֱ�߽�y���ڵ�E��0��2����
��1����������ߵĽ���ʽ��
��2����ͼ2������A��BE��ƽ���߽�����������һ��D����P����������λ���߶�AD�·���һ�����㣬����PA��EA��ED��PD�����ı���EAPD��������ֵ��
��3����ͼ3������AC������AOC�Ƶ�O��ʱ�뷽����ת������ת�е�������Ϊ��A��OC��������ת�����У�ֱ��OC����ֱ��BE���ڵ�Q������BOQΪ���������Σ���ֱ��д����Q�����꣮

���𰸡���1��y=![]() x2��
x2��![]() x��2����2��9����3��Q��������
x��2����2��9����3��Q��������![]() ����4��
����4��![]() ����2��1����4+
����2��1����4+![]() ����
����![]() ����
����
����������������� ![]() �ѵ�
�ѵ�![]() ����������
����������![]() �����
�����![]() ��ֵ����.
��ֵ����.
![]() ���ô���ϵ�������ֱ��BE�Ľ���ʽ���������ֱ��AD�Ľ���ʽ����
���ô���ϵ�������ֱ��BE�Ľ���ʽ���������ֱ��AD�Ľ���ʽ����![]() ��
��![]() ��ʾ��
��ʾ��![]() ,���䷽������������ֵ��
,���䷽������������ֵ��
��������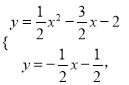 �����
�����![]() �����꣬
�����꣬ ![]() ���ֵ=
���ֵ=![]() ��
��
���������ı���EAPD��������ֵ��
![]() ����������������ۼ���.
����������������ۼ���.
�����������1����![]() ��������
��������![]() �ϣ�
�ϣ�
��![]()
���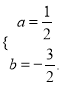
�������ߵĽ���ʽΪ![]()
��2������P��![]() �ύAD�ڵ�G��
�ύAD�ڵ�G��
��![]()
��ֱ��BE�Ľ���ʽΪ![]()
��AD��BE����ֱ��AD�Ľ���ʽΪ![]() ����
����![]() ���ɵ�
���ɵ�![]()
��ֱ��AD�Ľ���ʽΪ![]()
��![]() ��
��![]()
��![]()
�൱x=1ʱ��PG��ֵ������ֵΪ2��
��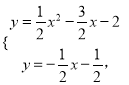 ���
���![]() ��
��![]()
��![]()
��![]() ���ֵ=
���ֵ=![]()
![]()
��AD��BE��
��![]()
��S�ı���APDE���=S��ADP���+![]()
��3������ͼ3��1�У���![]() ʱ����
ʱ����![]() ��T��
��T��
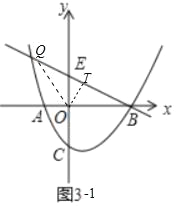
��![]()
��![]()
��![]()
��![]()
�ɵ�![]()
����ͼ3��2�У���![]() ʱ,
ʱ, 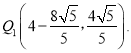
��![]() ʱ��
ʱ�� ![]()
��![]() ʱ��Q3
ʱ��Q3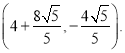
���������������������Q����Ϊ![]() ��
��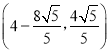 ��
��![]() ��
��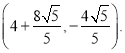



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У�������![]() ��m��0����x��Ľ���ΪA��B��
��m��0����x��Ľ���ΪA��B��
��1���������ߵĶ������ꣻ
��2���ᡢ�����궼�������ĵ�������㣮
����m��1ʱ�����߶�AB������ĸ�����
�����������ڵ�A��B֮��IJ������߶�AB��Χ�ɵ������ڣ������߽磩ǡ��6�����㣬��Ϻ�����ͼ����m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
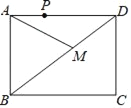
����Ŀ����ͼ������ABCD�У�AB=2![]() ��AD=6��PΪ��AD��һ�㣬��AP=2���ڶԽ���BD��Ѱ��һ��M��ʹAM+PM��С����AM+PM����СֵΪ_____��
��AD=6��PΪ��AD��һ�㣬��AP=2���ڶԽ���BD��Ѱ��һ��M��ʹAM+PM��С����AM+PM����СֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ӿ��ÿ���ļ��Ƴ�������Ӿ���ѷ�ʽ.��ʽһ���ȹ����Ա֤��ÿ�Ż�Ա֤100Ԫ��ֻ�ޱ��˵���ʹ�ã�ƾ֤��Ӿÿ���ٸ���5Ԫ����ʽ�����������Ա֤��ÿ����Ӿ����9Ԫ.
��1��ʲô����£�����Ա֤�벻��֤��һ����Ǯ��
��2��ʲô����£�����Ա֤�Ȳ���֤�����㣿
��3��ʲô����£�������Ա֤�ȹ�֤�����㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1���ȱ���ABC�ı߳�Ϊ4cm������D�ӵ�B������������BC�����ƶ�����ADΪ�����ȱ���ADE��
��1���ڵ�D�˶��Ĺ����У���E�ܷ��ƶ���ֱ��AB�ϣ����ܣ������ʱBD�ij��������ܣ���˵�����ɣ�
��2����ͼ2���ڵ�D�ӵ�B��ʼ�ƶ�����C�Ĺ����У��Եȱ���ADE�ı�AD��DEΪ����ADEF��
��ADEF������Ƿ������Сֵ�������ڣ���������Сֵ���������ڣ���˵�����ɣ�
������M��N��P�ֱ�ΪAE��AD��DE�϶��㣬ֱ��д��MN+MP����Сֵ��
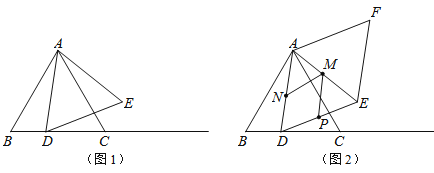
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С��ͬѧ��ѧУ��֯���������и����˽�������ס��С��450�������������ˮ��������������������50��������¾���ˮ������λ��t������������������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����ͼ����
�¾���ˮ������λ��t�� | Ƶ�� | �ٷֱ� |
2��x��3 | 2 | 4% |
3��x��4 | 12 | 24% |
4��x��5 | �� �� | �� �� |
5��x��6 | 10 | 20% |
6��x��7 | �� �� | 12% |
7��x��8 | 3 | 6% |
8��x��9 | 2 | 4% |
��1��������������е���Ϣ��ȫƵ���ֲ�����Ƶ���ֲ�ֱ��ͼ��
��2�������ͥ�¾���ˮ�������ڻ����4t��С��7t��Ϊ�е���ˮ����ͥ�������������С������ס��С���е���ˮ����ͥ��Լ�ж��ٻ���
��3�����¾���ˮ����2��x��3��8��x��9��������Χ�ڵ�������ͥ�������ȡ2���������оٷ�������״ͼ���б������ȡ����2����ͥ���Բ�ͬ��Χ�ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ��ij���ƶ���������ˮ�շѱ���ÿ��ÿ�µ���ˮ������10��ʱ��ˮ��Ϊÿ��1.2Ԫ������10��ʱ���������ְ�ÿ��1.8Ԫ�շѣ�����ij������5�·���ˮ![]() ��
��![]() ��Ӧ��ˮ��
��Ӧ��ˮ��![]() Ԫ��
Ԫ��
��1���![]() ��
��![]() ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
��2��ij��������5�·���ˮ16�֣�Ӧ��ˮ�Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ij��������ɫ���С���ʽ�������ijУ��ѧ��ȤС�����ʾ��������ʽ�����������ij�в��ֳ����������Ҫ���з�ʽ�������ʾ����������ֻ���������������ѡ��һ�ࣩ���������������Ƴ����²�������ͳ��ͼ��
���� | A | B | C | D | E |
���з�ʽ | �������� | ���� | ������ | ��ʿ | ˽�ҳ� |
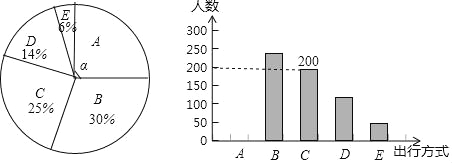
����������Ϣ���ش��������⣺
��1�����뱾���ʾ������������ �ˣ�����ѡ��B��������� �ˣ�
��2��������ͳ��ͼ�У���A���Ӧ����Բ�ĽǦ��Ķ���������ȫ����ͳ��ͼ��
��3������Լ��12���˳��У�����A��B��C��������з�ʽ����Ϊ����ɫ���С���ʽ������Ƹ��С���ɫ���С���ʽ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����:�ں�������д�ʵ���ʽ��������ţ���������ⷽ�̵Ĺ���
�ⷽ�̣�![]() ��
��
�⣺����ƽ������_____________________________________________
��������_____________________________________________________
��������̵�, ![]() ___________________,
___________________,![]() _____________________
_____________________
���飺��![]() ________�ֱ����ԭ�������ߣ����=_______________���ұ�=_________________,���ұ�__________��ߣ���֪
________�ֱ����ԭ�������ߣ����=_______________���ұ�=_________________,���ұ�__________��ߣ���֪![]() ________��________
________��________
��x=_________________�ֱ����ԭ�������ߣ����=________�����=_________________�ұߣ���֪![]() ________��________
________��________
���ԣ�ԭ���̵ĸ���___________________________
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com