
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图![]() 可以得到
可以得到![]()
![]() .请解答下列问题:
.请解答下列问题:

(1)写出图![]() 中所表示的数学等式;
中所表示的数学等式;

(2)利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同学打算用![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张相邻两边长为分别为
张相邻两边长为分别为![]() 、
、![]() 的长方形纸片拼出了一个面积为
的长方形纸片拼出了一个面积为 ![]() 长方形,那么他总共需要多少张纸片?
长方形,那么他总共需要多少张纸片?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知关于![]() 、
、![]() 的二元一次方程组
的二元一次方程组![]() (
(![]() 为常数).
为常数).
(1)求这个二元一次方程组的解(用含![]() 的代数式表示);
的代数式表示);
(2)若方程组的解![]() 、
、![]() 满足
满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若![]() ,设
,设![]() ,且m为正整数,求m的值.
,且m为正整数,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的函数,自变量
的函数,自变量![]() 的取值范围为
的取值范围为![]() ,下表是
,下表是![]() 与
与![]() 的几组对应值
的几组对应值
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | … |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系中,指出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象.

(2)根据画出的函数图象填空.
①该函数图象与![]() 轴的交点坐标为_____.
轴的交点坐标为_____.
②直接写出该函数的一条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(2,4),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标.
(2)画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2,并写出点A2的坐标.
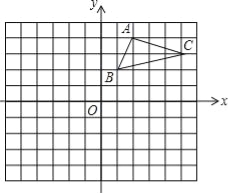
【答案】(1)作图见解析;点A1的坐标(2,﹣4);(2)作图见解析;点A2的坐标(﹣2,4).
【解析】
试题分析:(1)分别找出A、B、C三点关于x轴的对称点,再顺次连接,然后根据图形写出A点坐标;
(2)将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后,得到相应的对应点A2、B2、C2,连接各对应点即得△A2B2C2.
试题解析:(1)如图所示:点A1的坐标(2,﹣4);
(2)如图所示,点A2的坐标(﹣2,4).
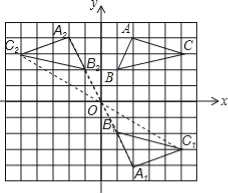
考点:1.作图-旋转变换;2.作图-轴对称变换.
【题型】解答题
【结束】
18
【题目】观察下面的点阵图和相应的等式,探究其中的规律:
(1)认真观察,并在④后面的横线上写出相应的等式.
![]()
①1=1 ②1+2=![]() =3 ③1+2+3=
=3 ③1+2+3=![]() =6 ④ …
=6 ④ …
(2)结合(1)观察下列点阵图,并在⑤后面的横线上写出相应的等式.
![]()
1=12②1+3=22③3+6=32④6+10=42⑤ …
(3)通过猜想,写出(2)中与第n个点阵相对应的等式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了促进生活垃圾的分类处理,将生活垃圾分为:可回垃圾、厨余垃圾、其他垃圾三类,分别记为A,B,C:并且设置了相应的垃圾箱,依次记为a,b,c.
(1)若将三类垃圾随机投入三个垃圾箱,请你用树形图的方法求垃圾投放正确的概率:
(2)为了调查小区垃圾分类投放情况,现随机抽取了该小区三类垃圾箱中总重500kg生活垃圾,数据如下(单位:)
a | b | c | |
A | 40 | 15 | 10 |
B | 60 | 250 | 40 |
C | 15 | 15 | 55 |
试估计“厨余垃圾”投放正确的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ACE中,CA=CE,∠CAE=30°,⊙O经过点C,且圆的直径AB在线段AE上.
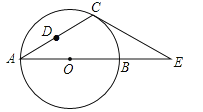
(1)试说明CE是⊙O的切线;
(2)若△ACE中AE边上的高为h,试用含h的代数式表示⊙O的直径AB;
(3)设点D是线段AC上任意一点(不含端点),连接OD,当![]() CD+OD的最小值为6时,求⊙O的直径AB的长.
CD+OD的最小值为6时,求⊙O的直径AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=OC,则四边形ABCD是什么特殊四边形?请直接给出你的结论,不必证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,点G在边BC的延长线上,CE平分∠BCD,CF平分∠GCD,EF∥BC交CD于点O.
(1)求证:OE=OF;
(2)若点O为CD的中点,求证:四边形DECF是矩形.
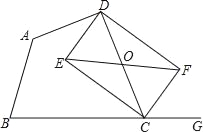
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com