
【题目】已知![]() 是
是![]() 的函数,自变量
的函数,自变量![]() 的取值范围为
的取值范围为![]() ,下表是
,下表是![]() 与
与![]() 的几组对应值
的几组对应值
| 0 | 1 | 2 | 3 | 3.5 | 4 | 4.5 | … |
| 1 | 2 | 3 | 4 | 3 | 2 | 1 | … |
小明根据学习函数的经验,利用上述表格所反映出的![]() 与
与![]() 之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
之间的变化规律,对该函数的图象与性质进行了探究.下面是小明的探究过程,请补充完整:
(1)如图,在平面直角坐标系中,指出了以上表中各对对应值为坐标的点. 根据描出的点,画出该函数的图象.

(2)根据画出的函数图象填空.
①该函数图象与![]() 轴的交点坐标为_____.
轴的交点坐标为_____.
②直接写出该函数的一条性质.
【答案】(1)见解析;(2)①(5,0);②见解析.
【解析】
(1)根据坐标,连接点即可得出函数图像;
(2)①根据图像,当x≥3时,根据两点坐标可得出函数解析式,进而可得出与![]() 轴的交点坐标;
轴的交点坐标;
②根据函数图像,相应的自变量的取值范围,可得出其性质.
(1) 如图:
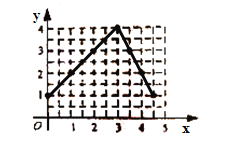
(2)①(5,0)
根据图像,当x≥3时,函数图像为一次函数,
设函数解析式为![]() ,将(3,4)和(4,2)两点代入,即得
,将(3,4)和(4,2)两点代入,即得
![]()
解得![]()
即函数解析式为![]()
与x轴的交点坐标为(5,0);
②答案不唯一.如下几种答案供参考:
当0≤x≤3时,函数值y随x值增大而增大;
当x≥3时,函数值y随x值增大而减小;
当x=3时,函数有最大值为4;
该函数没有最小值.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的顶点A、B分别在x轴与y轴上,已知OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC﹣CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
(1)当点P经过点C时,求直线DP的函数解析式;
(2)①求△OPD的面积S关于t的函数解析式;
②如图②,把长方形沿着OP折叠,点B的对应点B′恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师在黑板上书写了一个正确的演算过程,随后用手掌捂住了一个多项式,形式如下:
![]()
(1)求所捂的多项式;
(2)若x为正整数,任取x的几个值并求出所捂多项式的值,你能发现什么规律?
(3)若所捂多项式的值为144,请直接写出正整数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知单位长度为1的方格中有三角形ABC.
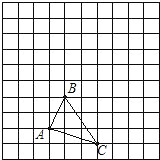
(1)请画出三角形ABC向上平移3格再向右平移2格后所得到的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标;
(3)求出三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC是一张等腰直角三角形纸板,∠C=Rt∠,AC=BC=2,在这张纸板中剪出一个尽可能大的正方形称为第1次剪取,记所得正方形面积为s1(如图1);在余下的Rt△ADE和Rt△BDF中,分别剪取正方形,得到两个相同的正方形,称为第2次剪取,并记这两个正方形面积和为s2(如图2);继续操作下去…;则第10次剪取时,s10= ;第2012次剪取后,余下的所有小三角形的面积之和是
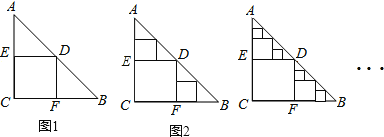
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(m﹣3)x﹣m(2m﹣3)=0
(1)证明:无论m为何值方程都有两个实数根;
(2)是否存在正数m,使方程的两个实数根的平方和等于26?若存在,求出满足条件的正数m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图是某种窗户的形状,其上部是半圆形,下部是边长相同的四个小正方形,已知下部的小正方形的边长为am,计算:
(1)窗户的面积;
(2)窗框的总长;
(3)若a=1,窗户上安装的是玻璃,玻璃每平方米25元,窗框每米20元,窗框的厚度不计,求制作这种窗户需要的费用是多少元(π取3.14,结果保留整数).
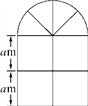
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图![]() 可以得到
可以得到![]()
![]() .请解答下列问题:
.请解答下列问题:

(1)写出图![]() 中所表示的数学等式;
中所表示的数学等式;

(2)利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同学打算用![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张相邻两边长为分别为
张相邻两边长为分别为![]() 、
、![]() 的长方形纸片拼出了一个面积为
的长方形纸片拼出了一个面积为 ![]() 长方形,那么他总共需要多少张纸片?
长方形,那么他总共需要多少张纸片?
查看答案和解析>>
科目:初中数学 来源: 题型:
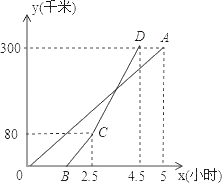
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com