
【题目】如图,四边形ABCD的对角线AC、BD交于点O,已知O是AC的中点,AE=CF,DF∥BE.
(1)求证:△BOE≌△DOF;
(2)若OD=OC,则四边形ABCD是什么特殊四边形?请直接给出你的结论,不必证明.

【答案】(1)详见解析;(2)若OD=OC,则四边形ABCD是矩形.
【解析】试题分析:(1)根据平行线的性质证明∠DFO=∠BEO,由O为AC的中点和AE=CF,证明OE=OF,根据ASA即可证得;
(2)根据全等三角形的性质,证明OB=OD,根据对角线互相平分且相等的四边形是矩形即可得证.
(1)证明:∵DF∥BE,
∴∠FDO=∠EBO,∠DFO=∠BEO,
∵O为AC的中点,即OA=OC,AE=CF,
∴OA﹣AE=OC﹣CF,即OE=OF,
在△BOE和△DOF中,
 ,
,
∴△BOE≌△DOF(AAS);
(2)若OD=OC,则四边形ABCD是矩形.
理由是:∵△BOE≌△DOF,
∴OB=OD,
又∵OA=OC,OD=OC,
∴OA=OC= OB=OD,
∴四边形ABCD是矩形.


科目:初中数学 来源: 题型:
【题目】如图,已知单位长度为1的方格中有三角形ABC.
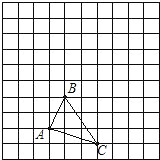
(1)请画出三角形ABC向上平移3格再向右平移2格后所得到的三角形A′B′C′;
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),然后写出点B,B′的坐标;
(3)求出三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图![]() 可以得到
可以得到![]()
![]() .请解答下列问题:
.请解答下列问题:

(1)写出图![]() 中所表示的数学等式;
中所表示的数学等式;

(2)利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同学打算用![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张相邻两边长为分别为
张相邻两边长为分别为![]() 、
、![]() 的长方形纸片拼出了一个面积为
的长方形纸片拼出了一个面积为 ![]() 长方形,那么他总共需要多少张纸片?
长方形,那么他总共需要多少张纸片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(-![]() )+(+
)+(+![]() )-(-
)-(-![]() )+(-
)+(-![]() )
)
(2)-54×![]() ÷(-
÷(-![]() )×
)×![]()
(3)-29×![]() -(-
-(-![]() )+29×(-
)+29×(-![]() )
)
(4)(-![]() -
-![]() +
+![]() )÷(-
)÷(-![]() )
)
(5)-42+3×(-2)2+(-6)÷(-![]() )2
)2
(6)∣-![]() ∣÷(
∣÷(![]() -
-![]() )-
)-![]() ×(-4)2
×(-4)2
查看答案和解析>>
科目:初中数学 来源: 题型:
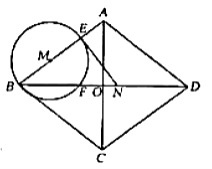
【题目】如图,菱形![]() 中,对角线
中,对角线![]() 相交于点
相交于点![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 的速度向点
的速度向点![]() 运动,同时动点
运动,同时动点![]() 从点
从点![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 的速度向点
的速度向点![]() 运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为
运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为![]() ,以点
,以点![]() 为圆心,
为圆心,![]() 为半径的⊙
为半径的⊙![]() 与射线
与射线![]() ,线段
,线段![]() 分别交于点
分别交于点![]() ,连接
,连接![]() .
.
(1)求![]() 的长(用含有
的长(用含有![]() 的代数式表示),并求出
的代数式表示),并求出![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,线段
为何值时,线段![]() 与⊙
与⊙![]() 相切?
相切?
(3)若⊙![]() 与线段
与线段![]() 只有一个公共点,求
只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一组数28、29.4、31.9、27、28.8、34.1、29.4的中位数、众数、极差分别是( )
A. ![]() 、
、![]() 、
、![]() B.
B. ![]() 、
、![]() 、
、![]()
C. 27、29、![]() D.
D. ![]() 、28、
、28、![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
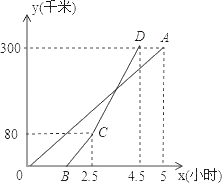
【题目】甲、乙两地相距300千米,一辆货车和一辆轿车先后从甲地出发向乙地,如图,线段OA表示货车离甲地距离y(千米)与时间x(小时)之间的函数关系;折线BCD表示轿车离甲地距离y(千米)与x(小时)之间的函数关系.请根据图象解答下列问题:
(1)轿车到达乙地后,货车距乙地多少千米?
(2)求线段CD对应的函数解析式.
(3)轿车到达乙地后,马上沿原路以CD段速度返回,求货车从甲地出发后多长时间再与轿车相遇(结果精确到0.01).
查看答案和解析>>
科目:初中数学 来源: 题型:
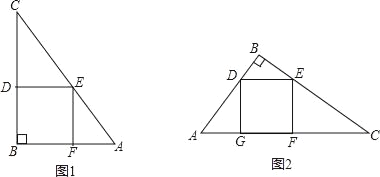
【题目】一块直角三角形木板的一条直角边AB长为1.5m,面积为1.5m2,工人师傅要把它加工成一个面积最大的正方形桌面,请甲、乙两位同学进行设计加工方案,甲设计方案如图1,乙设计方案如图2.你认为哪位同学设计的方案较好?试说明理由.(加工损耗忽略不计,计算结果中可保留分数)
查看答案和解析>>
科目:初中数学 来源: 题型:
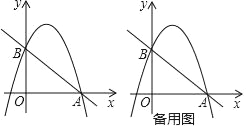
【题目】已知:如图,抛物线y=﹣x2+bx+C经过点B(0,3)和点A(3,0)
(1)求该抛物线的函数表达式和直线AB的函数表达式;
(2)若直线l⊥x轴,在第一象限内与抛物线交于点M,与直线AB交于点N,请在备用图上画出符合题意的图形,并求点M与点N之间的距离的最大值或最小值,以及此时点M,N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com