练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．在实数范围内分解因式：2x2-4x-3=2（x-$\frac{2+\sqrt{10}}{2}$）（x-$\frac{2-\sqrt{10}}{2}$）．

    分析 根公式法据解方程ax2+bx+c=0，可得方程的解，根据因式分解法可得ax2+bx+c=a（x-$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$）（x-$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$）．

    解答 解：由2x2-4x-3=0，得
    x=$\frac{2±\sqrt{10}}{2}$．
    原式=2（x2-2x-$\frac{3}{2}$）=2（x-$\frac{2+\sqrt{10}}{2}$）（x-$\frac{2-\sqrt{10}}{2}$），
    故答案为：2（x-$\frac{2+\sqrt{10}}{2}$）（x-$\frac{2-\sqrt{10}}{2}$）．

    点评 本题考查了因式分解，利用因式分解与相应方程两根的关系是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

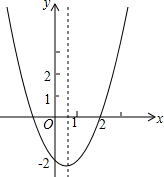    4．二次函数y=ax2+bx+c的图象如图所示，则下列结论中错误的是（　　）
    A．当x＜$\frac{1}{2}$，y随x的增大而减小B．函数有最小值
    C．a+b+c＜0D．当-1＜x＜2时，y＞0

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

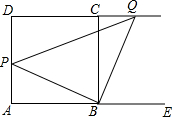    5．如图，在正方形ABCD中，点P是AD边上的一个动点，连接PB，过点B作一条射线与边DC的延长线交于点Q，使得∠QBE=∠PBC，其中E是边AB延长线上的点，连接PQ．
    （1）求证：△PBQ是等腰直角三角形；
    （2）若PQ2=PB2+PD2+1，求△PAB的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．某单位假日组织员工到A地旅游，现雇一辆载19人（不能超载）的客车，而到A地旅游有甲、乙两条路可走．有关数据如下：
    路程/km每百千米耗油量/L油价
    （元/L）    		过桥费/元票价
    元/人
    甲601432016
    乙64103512
    （1）设y1，y2（元）分别表示客车走甲、乙两条路线司机的收入，求y1，y2与乘客人数x（人）的关系式；
    （2）通过以上情况分析，你若是司机，应该选择那一条路线？请作出函数图象加以说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    9．如果P（-2，a）和Q（-3，b）都在正比例函数y=kx（k＜0）的图象上，那么a和b的大小是（　　）
    A．a＞bB．a=bC．a＜bD．以上都有可能

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．解方程：
    （1）（x-1）2-2（x-1）-8=0
    （2）2x2-$\sqrt{2}$x-1=0（配方法）

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    6．若y=$\frac{\sqrt{x-4}+\sqrt{4-x}}{2}$-2，则（x+y）2=4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．减去2x-y等于3z的式子是（　　）
    A．2x-y+3zB．2x-y-3zC．2x+y+3zD．2x+y-3z

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知x1、x2是方程x2-2（k+1）x+k2+2=0的另个实数根，且（x1+1）（x2+1）=8．求k的值．

    查看答案和解析>>

    同步练习册答案