
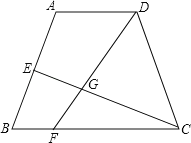
【题目】如图,已知等腰梯形ABCD中,AD∥BC,AD:BC=1:2,点E为边AB中点,点F是边BC上一动点,线段CE与线段DF交于点G.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)连接AG,在(1)的条件下,写出线段AG和线段DC的位置关系和数量关系,并说明理由;
(3)连接AG,若AD=2,AB=3,且△ADG与△CDF相似,求BF的长.
【答案】(1)![]() ;(2)AG∥DC,且
;(2)AG∥DC,且![]() ;理由见解析;(3)BF=1.
;理由见解析;(3)BF=1.
【解析】
(1)延长CE和DA,相交于M,根据平行线分线段成比例进行计算可以求出![]() 的值;
的值;
(2)在(1)的条件下,求出![]() ,根据对应线段的比相等可以得到AG与DC的位置和数量关系;
,根据对应线段的比相等可以得到AG与DC的位置和数量关系;
(3)根据∠ADG=∠DFC分两种情况讨论:①当∠AGD=∠FDC,即△ADG∽△CFD时,②当∠DAG=∠FDC时,分别求解即可.
解:(1)∵BF:FC=1:3,
∴设BF=k,则FC=3k,BC=4k,
∵AD:BC=1:2,
∴AD=2k,
如图:延长CE交DA的延长线于点M,
∵AD∥BC,
∴![]() ,且
,且![]() ,
,
∵点E为边AB中点,
∴AM=BC=4k,
∴DM=DA+AM=2k+4k=6k,
∴![]() ;
;
(2)AG∥DC,且![]() .
.
证明:∵AD∥BC,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴AG∥DC,
∴![]() ;
;
(3)∵ABCD是等腰梯形,AD=2,AD:BC=1:2,
∴BC=4,
∵AD∥BC,
∴∠ADG=∠DFC,
∵△ADG和△CDF相似,
∴∠AGD=∠FDC或∠DAG=∠FDC,
①当∠AGD=∠FDC,即△ADG∽△CFD时,有AG∥DC,延长CE交DA的延长线于点M,可得AM=4,
由![]() 得
得![]() ,
,
∴AG=2,
∵△ADG∽△CFD,
∴![]() ,即
,即![]() ,
,
∴CF=3,
∴BF=1;
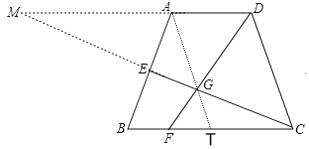
②当∠DAG=∠FDC时,延长AG交BC于点T,
∵∠ATB=∠DAG=∠FDC,∠B=∠C,
∴△ABT∽△FCD,
∴![]() ,
,
由AD∥BC得![]() ,
,
设BF=x,
则![]() ,
,
∴FT=![]() ,
,
∴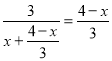 ,
,
整理得:2x2﹣4x+11=0,
∵△=16﹣88<0,
∴无实数根,即此情况不存在;
综上所述,BF=1.


科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张如图所示的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,按照同样的放置方式,
的长度变化时,按照同样的放置方式,![]() 始终保持不变,则
始终保持不变,则![]() ,
,![]() 满足的关系式为( )
满足的关系式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
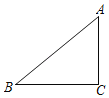
【题目】如图,Rt△ABC中,∠ACB=90°,AC=4,BC=5,点P为AC上一点,将△BCP沿直线BP翻折,点C落在C′处,连接AC′,若AC′∥BC,那么CP的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】华星商店准备从阳光机械厂购进甲、乙两种零件进行销售,若一个甲种零件的进价比一个乙种零件的进价多50元,用4000元购进甲种零件的数量是用1500元购进乙种零件的数量的2倍.
(1)求每个甲种零件,每个乙种零件的进价分别为多少元?
(2)华星商店甲种零件每件售价为260元,乙种零件每件售价为190元,商店根据市场需求.决定向该厂购进一批零件、且购进乙种零件的数量比购进甲种零件的数量的2倍还多4个,若本次购进的两种零件全部售出后,总获利不少于2400元、求该商店本次购进甲种零件至少是多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
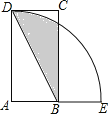
【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,E、F分别是AB、AD的中点,DE、BF相交于点G,连接BD、CG.给出以下结论:①∠BGD=120°;②BG+DG=CG;③△BDF≌△CGB;④S△ADE=![]() AB2.其中正确的有( )
AB2.其中正确的有( )
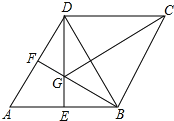
A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com