
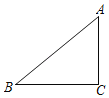
【题目】如图,Rt△ABC中,∠ACB=90°,AC=4,BC=5,点P为AC上一点,将△BCP沿直线BP翻折,点C落在C′处,连接AC′,若AC′∥BC,那么CP的长为__.
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境:在数学活动课上,老师出示了这样一个问题:如图1,在矩形ABCD中,AD=2AB,E是AB延长线上一点,且BE=AB,连接DE,交BC于点M,以DE为一边在DE的左下方作正方形DEFG,连接AM.试判断线段AM与DE的位置关系.
探究展示:勤奋小组发现,AM垂直平分DE,并展示了如下的证明方法:
证明:∵BE=AB,∴AE=2AB.
∵AD=2AB,∴AD=AE.
∵四边形ABCD是矩形,∴AD∥BC.
∴![]() .(依据1)
.(依据1)
∵BE=AB,∴![]() .∴EM=DM.
.∴EM=DM.
即AM是△ADE的DE边上的中线,
又∵AD=AE,∴AM⊥DE.(依据2)
∴AM垂直平分DE.
反思交流:
(1)①上述证明过程中的“依据1”“依据2”分别是指什么?
②试判断图1中的点A是否在线段GF的垂直平分线上,请直接回答,不必证明;
(2)创新小组受到勤奋小组的启发,继续进行探究,如图2,连接CE,以CE为一边在CE的左下方作正方形CEFG,发现点G在线段BC的垂直平分线上,请你给出证明;
探索发现:
(3)如图3,连接CE,以CE为一边在CE的右上方作正方形CEFG,可以发现点C,点B都在线段AE的垂直平分线上,除此之外,请观察矩形ABCD和正方形CEFG的顶点与边,你还能发现哪个顶点在哪条边的垂直平分线上,请写出一个你发现的结论,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校. 图中的折线表示清清的行程s(米)与所花时间t (分)之间的函数关系. 下列说法错误的是( )

A. 清清等公交车时间为3分钟 B. 清清步行的速度是80米/分
C. 公交车的速度是500米/分 D. 清清全程的平均速度为290米/分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两则材料,回答问题
材料一:我们将![]() +
+![]() 与
与![]() ﹣
﹣![]() 称为一对“对偶式”因为(
称为一对“对偶式”因为(![]() +
+![]() )(
)(![]()
![]() )=(
)=(![]() )2
)2![]() =a﹣b,所以构造“对偶式”相乘可以将
=a﹣b,所以构造“对偶式”相乘可以将![]() +
+![]() 与
与![]() ﹣
﹣![]() 中的“
中的“![]() ”去掉.
”去掉.
例如:已知![]()
![]() =2,求
=2,求![]() +
+![]() 的值,
的值,
解:(![]() )(
)(![]() +
+![]() )=(25﹣x)﹣(15﹣x)=10,
)=(25﹣x)﹣(15﹣x)=10,
∵![]() ﹣
﹣![]() =2,
=2,
∴![]() +
+![]() =5,
=5,
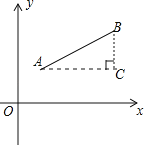
材料二:如图1,点A(x1,y1),点B(x2,y2),以AB为斜边作Rt△ABC,则C(x2,y1)AC=|x1﹣x2|,BC=|y1﹣y2|.所以AB=![]() .反之,可将代数式
.反之,可将代数式![]() 的值看作点A(x1,y1)到点B(x2,y2)的距离,例如
的值看作点A(x1,y1)到点B(x2,y2)的距离,例如![]() =
=![]() =
=![]() =
=![]() ,所以可将代数式
,所以可将代数式![]() 的值看作点(x,y)到点(1,﹣1)的距离.
的值看作点(x,y)到点(1,﹣1)的距离.
(1)利用材料一,解关于x的方程:![]()
![]() =5,其中x≤10;
=5,其中x≤10;
(2)利用材料二,求代数式![]() +
+ ![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范围;
的最小值,并求出此时y与x的函数关系式,写出x的取值范围;
(3)在(2)的条件下,设该式子取得最小值时的图形端点为M、N,直接写出将y与x的函数图象向左平移_____个单位时恰好经过点Q(﹣2,![]() ),并直接判定此时△MNQ的形状是______三角形.
),并直接判定此时△MNQ的形状是______三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
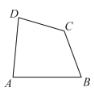
【题目】我们定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”,例如:如图,四边形![]() 是“等对角四边形”,
是“等对角四边形”,![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
(1)已知:在“等对角四边形”![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,求对角线
,求对角线![]() 的长;
的长;
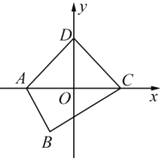
(2)已知:如图,在平面直角坐标系![]() 中,四边形
中,四边形![]() 是“等对角四边形”,其中
是“等对角四边形”,其中![]() ,
,![]() ,
,![]() ,点
,点![]() 在
在![]() 轴上,抛物线
轴上,抛物线![]() 过点
过点![]() 、
、![]() ,点
,点![]() 在抛物线上,满足
在抛物线上,满足![]() 的
的![]() 点至少有3个时,总有不等式
点至少有3个时,总有不等式![]() 成立,求
成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
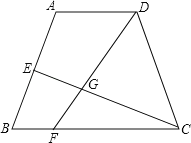
【题目】如图,已知等腰梯形ABCD中,AD∥BC,AD:BC=1:2,点E为边AB中点,点F是边BC上一动点,线段CE与线段DF交于点G.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)连接AG,在(1)的条件下,写出线段AG和线段DC的位置关系和数量关系,并说明理由;
(3)连接AG,若AD=2,AB=3,且△ADG与△CDF相似,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
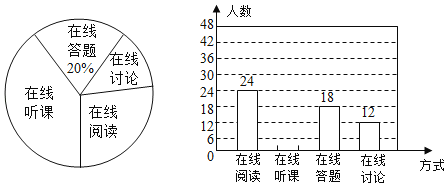
【题目】随着科技的进步和网络资源的丰富,在线学习已经成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解决学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调査,并根据调査结果绘制成如下两幅不完整的统计图.请你根据图中提供的信息解答下列问题:
(1)在这次调查中,一共抽取了多少名学生?
(2)通过计算补全条形统计图
(3)若该校共有学生2100人,请你估计该校对在线阅读最感兴趣的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级甲、乙两班各有学生50人,为了了解这两个班学生身体素质情况,进行了抽样调查,过程如下,请补充完整.
(1)收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试,测试成绩(百分制)如下:
甲班65 75 75 80 60 50 75 90 85 65
乙班90 55 80 70 55 70 95 80 65 70
(2)整理描述数据:按如下分数段整理、描述这两组样本数据:
成绩x 人数 班级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
甲班 | 1 | 3 | 3 | 2 | 1 |
乙班 | 2 | 1 | m | 2 | n |
在表中:m=______,n=______.
(3)分析数据:
①两组样本数据的平均数、中位数、众数如表所示:
班级 | 平均数 | 中位数 | 众数 |
甲班 | 72 | x | 75 |
乙班 | 72 | 70 | y |
在表中:x=______,y=______.
②若规定测试成绩在80分(含80分)以上的学生身体素质为优秀,请估计乙班50名学生中身体素质为优秀的学生有______人.
③现从甲班指定的2名学生(1男1女),乙班指定的3名学生(2男1女)中分别抽取1名学生去参加上级部门组织的身体素质测试,用树状图和列表法求抽到的2名同学是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
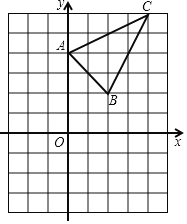
【题目】如图,△ABC在坐标平面内,三个顶点的坐标分别为A(0,4),B(2,2),C(4,6)(正方形网格中,每个小正方形的边长为1)
(1)画出△ABC向下平移5个单位得到的△A1B1C1,并写出点B1的坐标;
(2)以点O为位似中心,在第三象限画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为1:2,直接写出点C2的坐标和△A2B2C2的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com