
【题目】清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校. 图中的折线表示清清的行程s(米)与所花时间t (分)之间的函数关系. 下列说法错误的是( )

A. 清清等公交车时间为3分钟 B. 清清步行的速度是80米/分
C. 公交车的速度是500米/分 D. 清清全程的平均速度为290米/分
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】一家公司招考员工,每位考生要在A,B,C,D,E这5道试题中谁家抽出2道题回答,规定答对其中1题即为合格.
(1)请用树状图表示出所有可能的出题情形;
(2)已知某位考生只会答A,B两题,试求这位考生合格的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魔术师为大家表演魔术.他请观众想一个数,然后将这个数按以下步骤操作:

魔术师立刻说出观众想的那个数.
(1)如果小明想的数是-1,那么他告诉魔术师的结果应该是 ;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,若设一位观众想的数为a时,你能发现其中的奥妙吗?(请用式子或文字简单描述其中的规律)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在已知的ABC中,按以下步骤作图:
①分别以B,C为圆心,以大于 ![]() BC的长为半径作弧,两弧相交于两点M,N;
BC的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.若CD=AC,∠A=50°,则∠ACB的度数为( )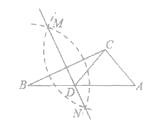
A.90°
B.95°
C.100°
D.105°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG; (2)OG= ![]() BC; ( 3)OGE是等边三角形; ( 4)SAOE=
BC; ( 3)OGE是等边三角形; ( 4)SAOE= ![]() S矩形ABCD
S矩形ABCD
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,AO=10,AB=8,沿直线CD折叠矩形OABC的一边BC,使点B落在OA边上的点E处,分别以OC,OA所在的直线为x轴,y轴建立平面直角坐标系,抛物线y=ax2+bx+c经过O,D,C三点.
(1)求AD的长及抛物线的解析式;
(2)一动点P从点E出发,沿EC以每秒2个单位长的速度向点C运动,同时动点Q从点C出发,沿CO以每秒1个单位长的速度向点O运动,当点P运动到点C时,两点同时停止运动,设运动时间为t秒,当t为何值时,以P,Q,C为顶点的三角形与ADE相似?
(3)点N在抛物线对称轴上,点M在抛物线上,是否存在这样的点M与点N,使以M,N,C,E为顶点的四边形是平行四边形?若存在,请直接写出点M与点N的坐标(不写求解过程);若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个数用大括号括起来,中间用逗号断开,如:{1,2,-3},{-2,7,![]() ,19},我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{5,0}就是一个好的集合.
,19},我们称之为集合,其中的数称为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数5-a也必是这个集合的元素,这样的集合我们称为好的集合.例如集合{5,0}就是一个好的集合.
(1)请你判断集合{1,2},{-2,1,2.5,4,7}是不是好的集合?
(2)请你再写出两个好的集合(不得与上面出现过的集合重复);
(3)写出所有好的集合中,元素个数最少的集合.
查看答案和解析>>
科目:初中数学 来源: 题型:
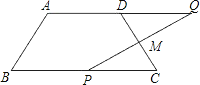
【题目】如图,在四边形ABCD中,AD∥BC,AD=5cm,BC=9cm.M是CD的中点,P是BC边上的一动点(P与B,C不重合),连接PM并延长交AD的延长线于Q.
(1)试说明△PCM≌△QDM.
(2)当点P在点B、C之间运动到什么位置时,四边形ABPQ是平行四边形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个长方形的三个顶点坐标分别为(﹣2,﹣2),(﹣2,3),(5,﹣2),则第四个顶点的坐标( )
A. (5,3) B. (3,5) C. (7,3) D. (3,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com