
【题目】魔术师为大家表演魔术.他请观众想一个数,然后将这个数按以下步骤操作:

魔术师立刻说出观众想的那个数.
(1)如果小明想的数是-1,那么他告诉魔术师的结果应该是 ;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,若设一位观众想的数为a时,你能发现其中的奥妙吗?(请用式子或文字简单描述其中的规律)
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,AD∥BC,点E在BC边的延长线上,CE=BC,连接AE,交CD边于点F,且CF=DF. 
(1)如图1,求证:AD=BC;
(2)如图2,连接BD、DE,若BD⊥DE,请判定四边形ABCD的形状,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格中建立平面直角坐标系如图,每个小正方形的边长均为1个单位长度.已知A(1,1)、B(3,4)和C(4,2).
(1)在图中标出点A、B、C.
(2)将点C向下平移3个单位到D点,将点A先向左平移3个单位,再向下平移1个单位到E点,在图中标出D点和E点.
(3)求△EBD的面积S△EBD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
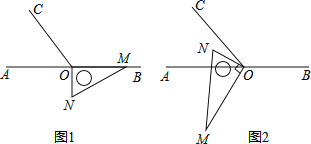
(1)将图1中的三角板绕点O按每秒10°的速度沿逆时针方向旋转一周.在旋转的过程中,假如第t秒时,OA、OC、ON三条射线构成相等的角,求此时t的值为多少?
(2)将图1中的三角板绕点O顺时针旋转图2,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
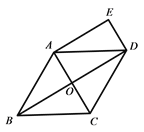
求证:四边形AODE是矩形;(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题:计算(2x3-3x2y-2xy2)-(x3-2xy2+y3)+(-x3+3x2y-y3)的值,其中x=-![]() ,y=-2.甲同学把“x=-
,y=-2.甲同学把“x=-![]() ”错抄成“x=
”错抄成“x=![]() ”.但他计算的结果是正确的,请你分析这是什么原因.
”.但他计算的结果是正确的,请你分析这是什么原因.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题: 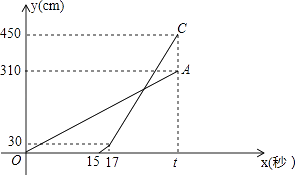
(1)乙比甲晚出发秒,乙提速前的速度是每秒cm,t=;
(2)当x为何值时,乙追上了甲?
(3)若两台机器人到达终点Q后迅速折返,并保持折返前的速度继续匀速行走返回到点P,乙比甲早到多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清清从家步行到公交车站台,等公交车去学校.下公交车后又步行了一段路程才到学校. 图中的折线表示清清的行程s(米)与所花时间t (分)之间的函数关系. 下列说法错误的是( )

A. 清清等公交车时间为3分钟 B. 清清步行的速度是80米/分
C. 公交车的速度是500米/分 D. 清清全程的平均速度为290米/分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,A(a,0),C(b,2),过C作CB⊥x轴,且满足(a+b)2+![]() =0.
=0.
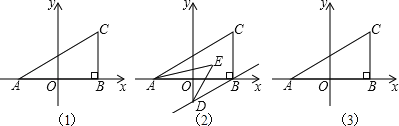
(1)求三角形ABC的面积.
(2)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,求∠AED的度数.
(3)在y轴上是否存在点P,使得三角形ABC和三角形ACP的面积相等?若存在,求出P点坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com