Question

【题目】如图（1），在平面直角坐标系中，A（a，0），C（b，2），过C作CB⊥x轴，且满足（a+b）2+=0．

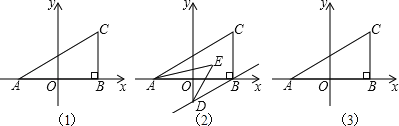
（1）求三角形ABC的面积．

（2）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，求∠AED的度数．

（3）在y轴上是否存在点P，使得三角形ABC和三角形ACP的面积相等？若存在，求出P点坐标；若不存在，请说明理由．

Answer 1

【答案】（1）4；（2）45°；（3）P点坐标为（0，3）或（0，﹣1）．

【解析】

试题分析：（1）根据非负数的性质得到a=﹣b，a﹣b+4=0，解得a=﹣2，b=2，则A（﹣2，0），B（2，0），C（2，2），即可计算出三角形ABC的面积=4；

（2）由于CB∥y轴，BD∥AC，则∠CAB=∠ABD，即∠3+∠4+∠5+∠6=90°，过E作EF∥AC，则BD∥AC∥EF，然后利用角平分线的定义可得到∠3=∠4=∠1，∠5=∠6=∠2，所以∠AED=∠1+∠2=×90°=45°；

（3）先根据待定系数法确定直线AC的解析式为y=x+1，则G点坐标为（0，1），然后利用S△PAC=S△APG+S△CPG进行计算．

解：（1）∵（a+b）2≥0，≥0，

∴a=﹣b，a﹣b+4=0，

∴a=﹣2，b=2，

∵CB⊥AB

∴A（﹣2，0），B（2，0），C（2，2）

∴三角形ABC的面积=×4×2=4；

（2）∵CB∥y轴，BD∥AC，

∴∠CAB=∠ABD，

∴∠3+∠4+∠5+∠6=90°，

过E作EF∥AC，

∵BD∥AC，

∴BD∥AC∥EF，

∵AE，DE分别平分∠CAB，∠ODB，

∴∠3=∠4=∠1，∠5=∠6=∠2，

∴∠AED=∠1+∠2=×90°=45°；

（3）存在．理由如下：

设P点坐标为（0，t），直线AC的解析式为y=kx+b，

把A（﹣2，0）、C（2，2）代入得，

解得，

∴直线AC的解析式为y=x+1，

∴G点坐标为（0，1），

∴S△PAC=S△APG+S△CPG=|t﹣1|2+|t﹣1|2=4，解得t=3或﹣1，

∴P点坐标为（0，3）或（0，﹣1）．