
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
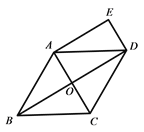
求证:四边形AODE是矩形;(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
【答案】(1)见解析(2)9![]()
【解析】试题分析:
(1)由已知易得四边形AODE是平行四边形,由四边形ABCD是菱形可得AC⊥BD,从而可得∠AOD=90°,由此可得平行四边形AODE是矩形;
(2)由四边形ABCD是菱形,∠BCD=120°易证△ABC是等边三角形,从而可得AC=AB=6,AO=3,结合AC⊥BD由勾股定理可得BO=3![]() ,则OD=3
,则OD=3![]() ,由此可得矩形AODE的面积为
,由此可得矩形AODE的面积为![]() .
.
试题解析:
(1)∵DE∥AC,AE∥BD,
∴四边形AODE是平行四边形,
∵在菱形ABCD中,AC⊥BD,
∴平行四边形AODE是矩形,
(2)∵∠BCD=120°,AB∥CD,
∴∠ABC=180°﹣120°=60°,
∵AB=BC,
∴△ABC是等边三角形,
∴OA=![]() ×4=2,
×4=2,
∵在菱形ABCD中,AC⊥BD,
∴由勾股定理OB=3![]() ,
,
∵四边形ABCD是菱形,
∴OD=OB=3![]() ,
,
∴四边形AODE的面积=OAOD=9![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在某市2016年“书香校园,经典诵读”比赛活动中,有32万名学生参加比赛活动,其中有8万名学生分别获得一、二、三等奖,从获奖学生中随机抽取部分,绘制成不完整的统计表(如表),请根据图表解答下列问题.
获奖等级 | 频数 |
一等奖 | a |
二等奖 | b |
三等奖 | 275 |

(1)表格中a的值为 , b的值为 .
(2)扇形统计图中表示获得一等奖的扇形的圆心角为度.
(3)估计全市有多少名学生获得三等奖?
查看答案和解析>>
科目:初中数学 来源: 题型:
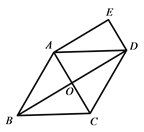
【题目】如图,在 ![]() ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.
ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.

(1)求证:四边形AFCE是平行四边形.
(2)若去掉已知条件的“∠DAB=60°,上述的结论还成立吗 ”若成立,请写出证明过程;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=6,AD=10,点E是边BC的中点,连接AE,若将△ABE沿AE翻折,点B落在点F处,连接FC,则tan∠BCF= . 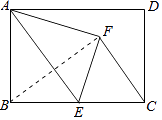
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】魔术师为大家表演魔术.他请观众想一个数,然后将这个数按以下步骤操作:

魔术师立刻说出观众想的那个数.
(1)如果小明想的数是-1,那么他告诉魔术师的结果应该是 ;
(2)如果小聪想了一个数并告诉魔术师结果为93,那么魔术师立刻说出小聪想的那个数是 ;
(3)观众又进行了几次尝试,魔术师都能立刻说出他们想的那个数,若设一位观众想的数为a时,你能发现其中的奥妙吗?(请用式子或文字简单描述其中的规律)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB. 
(1)判断CB与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,OP=1,求弦AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F,交AB于点E,点G是AE中点且∠AOG=30°,则下列结论正确的个数为( )
(1)DC=3OG; (2)OG= ![]() BC; ( 3)OGE是等边三角形; ( 4)SAOE=
BC; ( 3)OGE是等边三角形; ( 4)SAOE= ![]() S矩形ABCD
S矩形ABCD
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,四边形ABCD的四个顶点的坐标分别为A(0,0)、B(9,0)、C(7,5)、D(2,7).
(1)试计算四边形ABCD的面积;
(2)若将该四边形各顶点的横坐标都加2,纵坐标都加3,其面积怎么变化?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com