
【题目】如图,AB是⊙O的弦,点C在⊙O外,OC⊥OA,并交AB于点P,且CP=CB. 
(1)判断CB与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为3,OP=1,求弦AB的长.
【答案】
(1)解:∵OA=OB
∴∠OAB=∠OBA
∵CP=CB
∴∠CPB=∠CBP
在Rt△AOP中
∠A+∠APO=90°
∴∠OBA+∠CBP=90° 即:∠OBC=90°
∴OB⊥CB
又∵OB是半径
∴CB与⊙O相切
(2)解:设BC=CP=x
在Rt△OBC中
OC2=BC2+OB2
即:(x+1)2=x2+32
解之得:x=4,即:CP=4
在Rt△OBC中
AP= ![]() =
= ![]() =
= ![]()
作CH⊥AB于H
∵∠AOP=∠CHP=90°,∠APO=∠CPH
∴△OAP∽△HCP
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴HP= ![]()
∵CB=CP,CH⊥PB
∴PB=2PH= ![]()
![]()
∴AB=AP+PB= ![]()
![]() .
.
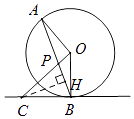
【解析】(1)根据等边对等角得∠CPB=∠CBP,根据垂直的定义得∠OBC=90°,即OB⊥CB,则CB与⊙O相切;(2)设BC=CP=x,在Rt△OBC中,根据勾股定理得出CP=4,再在Rt△OBC中,由勾股定理得出AP,作CH⊥AB,可证明△OAP∽△HCP,得出HP,由垂径定理得出PB=2PH,即可得出AB=AP+PB的长.
【考点精析】根据题目的已知条件,利用勾股定理的概念和垂径定理的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧.


科目:初中数学 来源: 题型:
【题目】在面积为12的平行四边形ABCD中,过点A作直线BC的垂线交直线BC于点E,过点A作直线CD的垂线交直线CD于点F,若AB=4,BC=6,则CE+CF的值为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB为直角,∠AOC为锐角,且OM平分∠BOC,ON平分∠AOC.
(1)如果∠AOC=50°,求∠MON的度数;
(2)如果∠AOC为任意一个锐角,你能求出∠MON的度数吗?若能,请求出来,若不能,说明为什么?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD中,对角线AC、BD相交于点O,DE∥AC,AE∥BD.
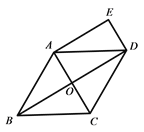
求证:四边形AODE是矩形;(2)若AB=6,∠BCD=120°,求四边形AODE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点从数轴上的原点开始,先向左移动![]() 到达
到达![]() 点,再向左移动
点,再向左移动![]() 到达
到达![]() 点,然后向右移动
点,然后向右移动![]() 到达
到达![]() 点
点
(1)用1个单位长度表示![]() ,请你在数轴上表示出
,请你在数轴上表示出![]() 、
、![]() 、
、![]() 三点的位置;
三点的位置;
![]()
(2)把点![]() 到点
到点![]() 的距离记为
的距离记为![]() ,则
,则![]() =_______
=_______ ![]() .
.
(3)若点![]() 以每秒
以每秒![]() 的速度向左移动,同时
的速度向左移动,同时![]() 、
、![]() 点分别以每秒
点分别以每秒![]() 、
、![]() 的速度向右移动.设移动时间为
的速度向右移动.设移动时间为![]() 秒,试探索:
秒,试探索: ![]() 的值是否会随着
的值是否会随着![]() 的变化而改变?请说明理由.
的变化而改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两台智能机器人从同一地点P出发,沿着笔直的路线行走了450cm到点Q.甲比乙先出发,乙出发一段时间后速度提高为原来的2倍.甲匀速走完全程.两机器人行走的路程y(cm)与时间x(s)之间的函数图象如图所示.根据图象所提供的信息解答下列问题: 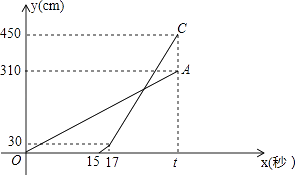
(1)乙比甲晚出发秒,乙提速前的速度是每秒cm,t=;
(2)当x为何值时,乙追上了甲?
(3)若两台机器人到达终点Q后迅速折返,并保持折返前的速度继续匀速行走返回到点P,乙比甲早到多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)15+(-![]() )-15-(-0.25) (2) (-81)÷
)-15-(-0.25) (2) (-81)÷![]() ×
×![]() ÷(-32)
÷(-32)
(3)29![]() ×(-12) (4)25×
×(-12) (4)25×![]() -(-25)×
-(-25)×![]() +25×(-
+25×(-![]() )
)
(5)-24-(-4)2 ×(-1)+(-3)3 (6)3.25-[(-![]() )-(-
)-(-![]() )+(-
)+(-![]() )+
)+![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com