
【题目】阅读下列两则材料,回答问题
材料一:我们将![]() +
+![]() 与
与![]() ﹣
﹣![]() 称为一对“对偶式”因为(
称为一对“对偶式”因为(![]() +
+![]() )(
)(![]()
![]() )=(
)=(![]() )2
)2![]() =a﹣b,所以构造“对偶式”相乘可以将
=a﹣b,所以构造“对偶式”相乘可以将![]() +
+![]() 与
与![]() ﹣
﹣![]() 中的“
中的“![]() ”去掉.
”去掉.
例如:已知![]()
![]() =2,求
=2,求![]() +
+![]() 的值,
的值,
解:(![]() )(
)(![]() +
+![]() )=(25﹣x)﹣(15﹣x)=10,
)=(25﹣x)﹣(15﹣x)=10,
∵![]() ﹣
﹣![]() =2,
=2,
∴![]() +
+![]() =5,
=5,
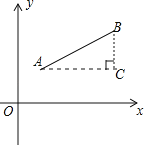
材料二:如图1,点A(x1,y1),点B(x2,y2),以AB为斜边作Rt△ABC,则C(x2,y1)AC=|x1﹣x2|,BC=|y1﹣y2|.所以AB=![]() .反之,可将代数式
.反之,可将代数式![]() 的值看作点A(x1,y1)到点B(x2,y2)的距离,例如
的值看作点A(x1,y1)到点B(x2,y2)的距离,例如![]() =
=![]() =
=![]() =
=![]() ,所以可将代数式
,所以可将代数式![]() 的值看作点(x,y)到点(1,﹣1)的距离.
的值看作点(x,y)到点(1,﹣1)的距离.
(1)利用材料一,解关于x的方程:![]()
![]() =5,其中x≤10;
=5,其中x≤10;
(2)利用材料二,求代数式![]() +
+ ![]() 的最小值,并求出此时y与x的函数关系式,写出x的取值范围;
的最小值,并求出此时y与x的函数关系式,写出x的取值范围;
(3)在(2)的条件下,设该式子取得最小值时的图形端点为M、N,直接写出将y与x的函数图象向左平移_____个单位时恰好经过点Q(﹣2,![]() ),并直接判定此时△MNQ的形状是______三角形.
),并直接判定此时△MNQ的形状是______三角形.
【答案】(1)x=9;(2)y=﹣7x+11(1≤x≤2);最小值为5![]() ;(3)
;(3)![]() ,锐角.
,锐角.
【解析】
(1)根据(![]() +
+![]() )(
)(![]() ﹣
﹣![]() )=25﹣x﹣10+x=15,
)=25﹣x﹣10+x=15,![]() +
+![]() =5,推出
=5,推出![]() ﹣
﹣![]() =3,求出
=3,求出![]() ,
,![]() 的值即可解决问题.
的值即可解决问题.
(2)由代数式![]() =
=![]()
![]() ,可知求代数式
,可知求代数式![]()
![]() 的最小值,可以转化为找一点P(x,y),使得点P到M(1,4)和N(2,﹣3)的距离之和最小,这个最小值是线段MN的长,点P在线段MN上,由此即可解决问题.
的最小值,可以转化为找一点P(x,y),使得点P到M(1,4)和N(2,﹣3)的距离之和最小,这个最小值是线段MN的长,点P在线段MN上,由此即可解决问题.
(3)设平移后的直线的解析式为y=﹣7x+m,把点Q(﹣2,![]() )代入,可得平移后的直线的解析式为y=﹣7x﹣
)代入,可得平移后的直线的解析式为y=﹣7x﹣![]() ,求出两直线与x轴的交点坐标,即可求出平移的距离,再利用两点间距离公式,结合勾股定理的逆定理即可解决问题.
,求出两直线与x轴的交点坐标,即可求出平移的距离,再利用两点间距离公式,结合勾股定理的逆定理即可解决问题.
解:(1)∵(![]() +
+![]() )(
)(![]() ﹣
﹣![]() )=25﹣x﹣10+x=15,
)=25﹣x﹣10+x=15, ![]() +
+![]() =5,
=5,
∴![]() ﹣
﹣![]() =3,
=3,
∴![]() =4,
=4,![]() =1,
=1,
∴x=9.
(2)∵代数式![]() +
+![]()
=![]() +
+![]() ,
,
∴求代数式![]() +
+![]() 的最小值,可以转化为找一点P(x,y),使得点P到M(1,4)和N(2,﹣3)的距离之和最小,这个最小值是线段MN的长,点P在线段MN上,
的最小值,可以转化为找一点P(x,y),使得点P到M(1,4)和N(2,﹣3)的距离之和最小,这个最小值是线段MN的长,点P在线段MN上,
∵MN=![]() =5
=5![]() ,
,
∴代数式![]() +
+![]() 的最小值为5
的最小值为5![]() ,
,
设直线MN的解析式为y=kx+b,则有![]() ,
,
解得![]() ,
,
∴此时y与x的函数关系式:y=﹣7x+11(1≤x≤2).
(3)设平移后的直线的解析式为y=﹣7x+m,
把点Q(﹣2,![]() )代入得到:
)代入得到:![]() =14+m,
=14+m,
m=﹣![]() ,
,
∴平移后的直线的解析式为y=﹣7x﹣![]() ,
,
∵直线y=﹣7x+11交x轴于(![]() ,0),直线y=﹣7x﹣
,0),直线y=﹣7x﹣![]() 交x轴于(﹣
交x轴于(﹣![]() ,0),
,0),
∴平移的距离=![]() +
+![]() =
=![]() ,
,
∵M(1,4),N(2,﹣3),Q(﹣2,![]() ),
),
∴MN2=50,MQ2=32+(![]() )2,NQ2=42+(
)2,NQ2=42+(![]() )2,
)2,
∴MN>MQ,MN>NQ,
∵MQ2+NQ2=25+![]() <50,
<50,
∴∠MQN<90°,
∴△MNQ是锐角三角形.
故答案为![]() ,锐角.
,锐角.


科目:初中数学 来源: 题型:
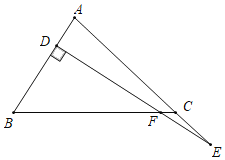
【题目】如图,在△ABC中,∠ACB=45°,点D在AB上,点E在AC的延长线上,ED⊥AB,ED交BC于点F,AB=DF,3DF=5EF,CF=l,则AC=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
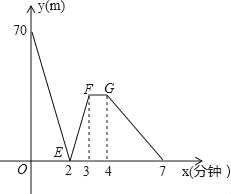
【题目】有一科技小组进行了机器人行走性能试验,在试验场地有A、B、C三点顺次在同一笔直的赛道上,甲、乙两机器人分别从A、B两点同时同向出发,历时7分钟同时到达C点,乙机器人始终以60米/分的速度行走,如图是甲、乙两机器人之间的距离y(米)与他们的行走时间x(分钟)之间的函数图象,请结合图象,回答下列问题:
(1)A、B两点之间的距离是 米,甲机器人前2分钟的速度为 米/分;
(2)若前3分钟甲机器人的速度不变,求线段EF所在直线的函数解析式;
(3)若线段FG∥x轴,则此段时间,甲机器人的速度为 米/分;
(4)求A、C两点之间的距离;
(5)若前3分钟甲机器人的速度不变,直接写出两机器人出发多长时间相距28米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
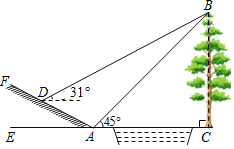
【题目】如图,小明为了测量小河对岸大树BC的高度,他在点A测得大树顶端B的仰角为45°,沿斜坡走3![]() 米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
米到达斜坡上点D,在此处测得树顶端点B的仰角为31°,且斜坡AF的坡比为1:2.
(1)求小明从点A到点D的过程中,他上升的高度;
(2)大树BC的高度约为多少米?(参考数据:sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五张如图所示的长为![]() ,宽为
,宽为![]() 的小长方形纸片,按如图的方式不重叠地放在矩形
的小长方形纸片,按如图的方式不重叠地放在矩形![]() 中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为
中,未被覆盖的部分(两个矩形)用阴影表示.设左上角与右下角的阴影部分的面积的差为![]() ,当
,当![]() 的长度变化时,按照同样的放置方式,
的长度变化时,按照同样的放置方式,![]() 始终保持不变,则
始终保持不变,则![]() ,
,![]() 满足的关系式为( )
满足的关系式为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
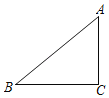
【题目】如图,Rt△ABC中,∠ACB=90°,AC=4,BC=5,点P为AC上一点,将△BCP沿直线BP翻折,点C落在C′处,连接AC′,若AC′∥BC,那么CP的长为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
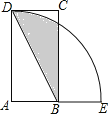
【题目】如图,四边形ABCD为矩形,以A为圆心,AD为半径的弧交AB的延长线于点E,连接BD,若AD=2AB=4,则图中阴影部分的面积为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”倡议提出五年多来,交通、通信、能源等各项相关建设取得积极进展,也为增进各国民众福祉提供了新的发展机遇.下图是2017年“一年一路”沿线部分国家的通信设施现状统计图.
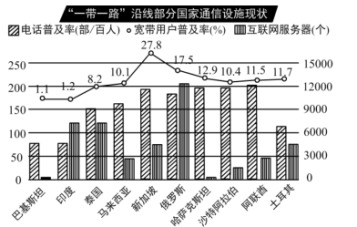
根据统计图提供的信息,下列推断合理的是( ).
A.互联网服务器拥有个数最多的国家是阿联酋
B.宽带用户普及率的中位数是11.05%
C.有8个国家的电话普及率能够达到平均每人1部
D.只有俄罗斯的三项指标均超过了相应的中位数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com