练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】“一带一路”倡议提出五年多来，交通、通信、能源等各项相关建设取得积极进展，也为增进各国民众福祉提供了新的发展机遇．下图是2017年“一年一路”沿线部分国家的通信设施现状统计图．

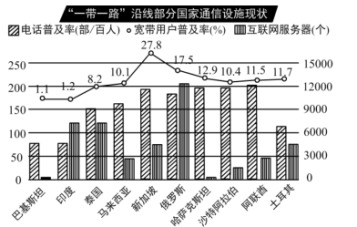
    根据统计图提供的信息，下列推断合理的是（ ）．

    A.互联网服务器拥有个数最多的国家是阿联酋

    B.宽带用户普及率的中位数是11.05%

    C.有8个国家的电话普及率能够达到平均每人1部

    D.只有俄罗斯的三项指标均超过了相应的中位数

    【答案】C

    【解析】

    由题意根据统计图提供的信息，利用众数、中位数以及平均数的求解方法进行分析判断.

    解：A选项：互联网服务器拥有个数最多的国家是俄罗斯，原说法错误；

    B选项：宽带用户普及率从小到大排列，依次是1．1，1．2，8．2，10．1，10．4，11．5，11．7，12．9，17．5，27．8，故中位数为，原说法错误；

    C选项：电话普及率在100部/百人的有8个国家，即有8个国家的电话普及率能够达到平均每人1部，正确；

    D选项：明显可以得到，新加坡的三项指标也均超过了相应的中位数，原说法错误．

    故选：C．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】阅读下列两则材料，回答问题

    材料一：我们将+与﹣称为一对“对偶式”因为（+）（）＝（）2＝a﹣b，所以构造“对偶式”相乘可以将+与﹣中的“”去掉．

    例如：已知＝2，求+的值，

    解：（）（+）＝（25﹣x）﹣（15﹣x）＝10，

    ∵﹣＝2，

    ∴+＝5，

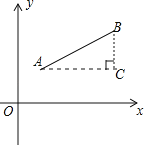
    材料二：如图1，点A（x1，y1），点B（x2，y2），以AB为斜边作Rt△ABC，则C（x2，y1）AC＝|x1﹣x2|，BC＝|y1﹣y2|．所以AB＝．反之，可将代数式的值看作点A（x1，y1）到点B（x2，y2）的距离，例如＝＝＝，所以可将代数式的值看作点（x，y）到点（1，﹣1）的距离．

    （1）利用材料一，解关于x的方程：＝5，其中x≤10；

    （2）利用材料二，求代数式+ 的最小值，并求出此时y与x的函数关系式，写出x的取值范围；

    （3）在（2）的条件下，设该式子取得最小值时的图形端点为M、N，直接写出将y与x的函数图象向左平移_____个单位时恰好经过点Q（﹣2，），并直接判定此时△MNQ的形状是______三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校八年级甲、乙两班各有学生50人，为了了解这两个班学生身体素质情况，进行了抽样调查，过程如下，请补充完整．

    （1）收集数据:从甲、乙两个班各随机抽取10名学生进行身体素质测试，测试成绩（百分制）如下：

    甲班65 75 75 80 60 50 75 90 85 65

    乙班90 55 80 70 55 70 95 80 65 70

    （2）整理描述数据:按如下分数段整理、描述这两组样本数据：

    成绩x

    人数

    班级

    50≤x＜60

    60≤x＜70

    70≤x＜80

    80≤x＜90

    90≤x≤100

    甲班

    1

    3

    3

    2

    1

    乙班

    2

    1

    m

    2

    n

    在表中：m=______，n=______．

    （3）分析数据:

    ①两组样本数据的平均数、中位数、众数如表所示：

    班级

    平均数

    中位数

    众数

    甲班

    72

    x

    75

    乙班

    72

    70

    y

    在表中：x=______，y=______．

    ②若规定测试成绩在80分（含80分）以上的学生身体素质为优秀，请估计乙班50名学生中身体素质为优秀的学生有______人．

    ③现从甲班指定的2名学生（1男1女），乙班指定的3名学生（2男1女）中分别抽取1名学生去参加上级部门组织的身体素质测试，用树状图和列表法求抽到的2名同学是1男1女的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】近年，《中国诗词大会》、《朗读者》，《经典咏流传》、《国家宝藏》等文化类节目相继走红，被人们称为“清流综艺”，六中上智中学某兴趣小组想了解全校学生对这四个节目的喜爱情况，随机抽取了部分学生进行调查统计，要求每名学生选出一个自己最喜爱的节目，并将调查结果给制成如下统计图（其中《中国诗词大会》，《朗读者》，《经典咏流传》，《国家宝藏》分别用A，B，C．D表示），请你结合图中信息解答下列问题：

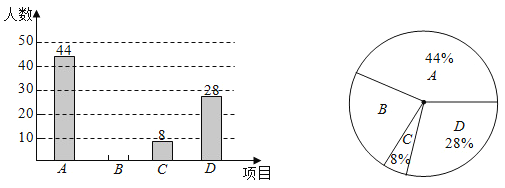
    （1）本次调查的学生人数是　 　人：

    （2）请把条形统计图补充完整．

    （3）在扇形统计图中，B对应的圆心角的度数是　 　．

    （4）已知六中上智中学共有3200名学生，请根据样本估计全校最喜爱《朗读者》的人数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知△ABC，∠C = 90°，．D为BC上一点，且到A，B两点的距离相等．

    （1）用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；

    （2）连结AD，若∠B = 35°，求∠CAD的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC 内接于⊙O，∠B=60°，CD 是⊙O 的直径，点 P 是 CD 延长线上的一点且 AP=AC．

    （1）求证：PA 是⊙O 的切线；

    （2）若，，求⊙O的半径

    查看答案和解析>>

    科目：初中数学 来源： 题型：

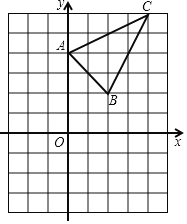
    【题目】如图，△ABC在坐标平面内，三个顶点的坐标分别为A（0，4），B（2，2），C（4，6）（正方形网格中，每个小正方形的边长为1）

    （1）画出△ABC向下平移5个单位得到的△A1B1C1，并写出点B1的坐标；

    （2）以点O为位似中心，在第三象限画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为1：2，直接写出点C2的坐标和△A2B2C2的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某省对部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，级：对学习很感兴趣；级：对学习较感兴趣；级：对学习不感兴趣），并将调查结果绘制成图①和图②不完整的统计图．请根据图中提供的信息，解答下列问题：

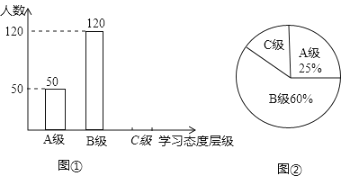
    （1）此次抽样调查中，共调查了______名学生；

    （2）将图①补充完整；

    （3）求出图②中级所占的圆心角的度数；

    （4）根据抽样调查结果，请你估计该省近40000名八年级学生中大约有多少名学生学习态度达标（达标包括级和级）？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

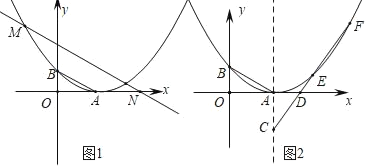
    【题目】在平面直角坐标系中，抛物线yx2沿x轴正方向平移后经过点A（x1，y2），B（x2，y2），其中x1，x2是方程x2﹣2x＝0的两根，且x1＞x2，

    （1）如图．求A，B两点的坐标及平移后抛物线的解析式；

    （2）平移直线AB交抛物线于M，交x轴于N，且，求△MNO的面积；

    （3）如图，点C为抛物线对称轴上顶点下方的一点，过点C作直线交抛物线于E、F，交x轴于点D，探究的值是否为定值？如果是，求出其值；如果不是，请说明理由．

    查看答案和解析>>

    同步练习册答案