
【题目】已知:如图,直线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,线段
,线段![]() 的长是方程
的长是方程![]() 的一个根,请解答下列问题:
的一个根,请解答下列问题:
(1)求点![]() 的坐标;
的坐标;
(2)双曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,
上,![]() ,直线
,直线![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 在直线
在直线![]() 上,在直线
上,在直线![]() 上的坐标平面内是否存在点
上的坐标平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请求出点
为顶点的四边形是矩形?若存在,请求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
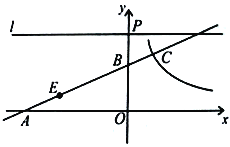
【答案】(1)![]() ;(2)10;(3)
;(2)10;(3)![]() 或
或![]()
【解析】
(1)解方程x2-7x-8=0得:x=8,或x=-1,得出OA=8,A(-8,0),代入y=![]() x+b求出b=4,即可得出B(0,4);
x+b求出b=4,即可得出B(0,4);
(2)在Rt△AOB中,由勾股定理求出AB= ![]() ,过点C作CH⊥x轴于H,则CH∥OB,由平行线得出△AOB∽△AHC,得出
,过点C作CH⊥x轴于H,则CH∥OB,由平行线得出△AOB∽△AHC,得出![]() ,求出CH=5,AH=10,得出OH=2,C(2,5),代入双曲线得出k=10即可;
,求出CH=5,AH=10,得出OH=2,C(2,5),代入双曲线得出k=10即可;
(3)先求出点E的坐标,再分三种情况讨论计算即可得出结论.
解:(1)解方程![]() 得
得![]() 或
或![]() .
.
∵线段![]() 的长是方程
的长是方程![]() 的一个根,
的一个根,
∵![]() 的长是正数
的长是正数
∴![]() ,
,
∴![]() .
.
将![]() 代入
代入![]() ,得
,得![]() ,
,
∴![]() ,
,
∴![]() .·
.·
(2)在![]() 中,
中,![]() ,
,
∴![]() .
.
如图,过点![]() 作
作![]() 轴于点
轴于点![]() ,则
,则![]() ,
,
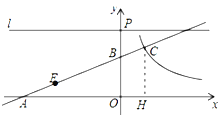
∴![]()
∴ ![]() 即
即 ![]()
解得![]() ,
,
∴![]() ,
,
∴![]() .
.
∵双曲线(![]() )经过点
)经过点![]() ,
,
∴![]() ·
·
(3)存在
①当![]() 为以点
为以点![]() 为顶点的矩形的一边时,过点
为顶点的矩形的一边时,过点![]() 作
作![]() 轴于点
轴于点![]() ,作
,作![]() 交直线
交直线![]() 于点
于点![]() ,如图所示,
,如图所示,
∴![]() ,
,
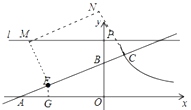
∴![]()
∴ ![]()
∴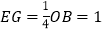 ,
,![]()
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴设直线![]() 的函数表达式为
的函数表达式为![]() ,
,
把![]() 代入,得
代入,得![]() ,
,
解得![]() ,
,
∴直线![]() 的函数表达式为
的函数表达式为![]()
当![]() 时,
时,![]() ,
,
∴![]() ,
,
∴![]() .(注:也可以用三角形相似求解
.(注:也可以用三角形相似求解![]()
![]() ∴
∴![]() 如图3
如图3
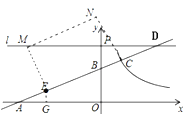
图3
∵![]()
∴点![]() 的坐标为
的坐标为![]() ;(点的平移)
;(点的平移)
当![]() 为以点
为以点![]() 为顶点的矩形的一边时,同理得出满足条件的另一点
为顶点的矩形的一边时,同理得出满足条件的另一点![]() 的坐标为
的坐标为![]() ;
;
②当![]() 为以点
为以点![]() 为顶点的矩形的对角线时,点
为顶点的矩形的对角线时,点![]() 在直线
在直线![]() 的下方,不符合题意。
的下方,不符合题意。
∴满足条件的![]() 的坐标为
的坐标为![]() 或
或![]() ;
;


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】(题文)如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.
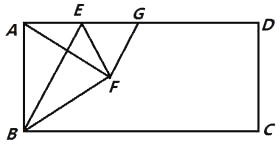
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
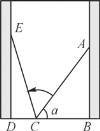
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A1,A2,A3,… 和B1,B2,B3,… 分别在直线![]() 和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
和x轴上.△OA1 B1,△B1 A2 B2,△B2 A3 B3,…都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是( )
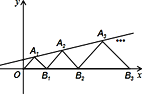
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() 为直径,
为直径,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线分别交
的平行线分别交![]() ,
,![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
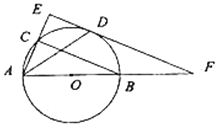
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)设![]() ,
,![]() ,试用含
,试用含![]() ,
,![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经营一种文化衫,已知成批购进时的单价是20元.调查发现:销售单价是30元时,月销售量是230件,而销售单价每上涨1元,月销售量就减少10件,但每件文化衫售价不能高于40元.设每件文化衫的销售单价上涨了![]() 元时(
元时(![]() 为正整数),月销售利润为
为正整数),月销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围.
的取值范围.
(2)每件文化衫的售价定为多少元时可使月销售利润最大?最大的月利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,对角线AC、BD相交于O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①BE⊥AC;②EG=GF;③△EFG≌△GBE;④EA平分∠GEF;⑤四边形BEFG是菱形.其中正确的是( )
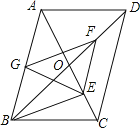
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com