
【题目】已知二次函数![]() (h为常数),在自变量
(h为常数),在自变量![]() 的值满足
的值满足![]() 的情况下,与其对应的函数值
的情况下,与其对应的函数值![]() 的最大值为0,则
的最大值为0,则![]() 的值为( )
的值为( )
A. ![]() 和
和![]() B.
B. ![]() 和
和![]() C.
C. ![]() 和
和![]() D.
D. ![]() 和
和![]()
【答案】A
【解析】
由解析式可知该函数在x=h时取得最大值1、x<h时,y随x的增大而增大、当x>h时,y随x的增大而减小,根据1≤x≤4时,函数的最大值为0,可分如下两种情况:①若h<1≤x≤4,x=1时,y取得最大值0;②若1≤x≤4<h,当x=4时,y取得最大值0,分别列出关于h的方程求解即可.
∵x<h时,y随x的增大而增大、当x>h时,y随x的增大而减小,
∴①若h<1≤x≤4,x=1时,y取得最大值0,
可得:-(1-h)2+4=0,
解得:h=-1或h=3(舍);
②若1≤x≤4<h,当x=4时,y取得最大值0,
可得:-(4-h)2+4=0,
解得:h=2(舍)或h=6.
综上,h的值为-1或6,
故选:A.


科目:初中数学 来源: 题型:
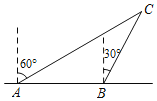
【题目】如图所示,一艘轮船在近海处由西向东航行,点C处有一灯塔,灯塔附近30海里的圆形区域内有暗礁,轮船在A处测得灯塔在北偏东60°方向上,轮船又由A向东航行40海里到B处,测得灯塔在北偏东30°方向上.
(1)求轮船在B处时到灯塔C处的距离是多少?
(2)若轮船继续向东航行,有无触礁危险?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l为y=![]() x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3…,按此作法进行下去,则
x,过点A1(1,0)作A1B1⊥x轴,与直线l交于点B1,以原点O为圆心,OB1长为半径画圆弧交x轴于点A2;再作A2B2⊥x轴,交直线l于点B2,以原点O为圆心,OB2长为半径画圆弧交x轴于点A3…,按此作法进行下去,则![]() 的长为______(用含n,π的式子表示).
的长为______(用含n,π的式子表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
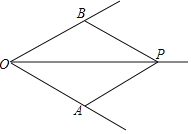
【题目】已知:如图,做![]() 的平分线
的平分线![]() ,在
,在![]() 的两边上分别截取
的两边上分别截取![]() ,再以点
,再以点![]() 为圆心,线段
为圆心,线段![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)尺规作图:作线段![]() 的垂直平分线
的垂直平分线![]() ,分别交
,分别交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() (不写做法,保留作图痕迹);
(不写做法,保留作图痕迹);
(3)当![]() 时,判断
时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四位同学进行一次乒乓球单打比赛,要从中选出两位同学打第一场比赛.
(1)请用树状图法或列表法,求恰好选中甲、乙两位同学的概率.
(2)若已确定甲打第一场,再从其余三位同学中随机选取一位,求恰好选中乙同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
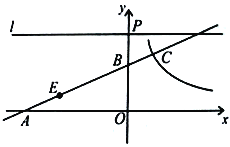
【题目】已知:如图,直线![]() 与
与![]() 轴负半轴交于点
轴负半轴交于点![]() ,与
,与![]() 轴正半轴交于点
轴正半轴交于点![]() ,线段
,线段![]() 的长是方程
的长是方程![]() 的一个根,请解答下列问题:
的一个根,请解答下列问题:
(1)求点![]() 的坐标;
的坐标;
(2)双曲线![]() 与直线
与直线![]() 交于点
交于点![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,点![]() 在线段
在线段![]() 上,
上,![]() ,直线
,直线![]() 轴,垂足为
轴,垂足为![]() ,点
,点![]() 在直线
在直线![]() 上,在直线
上,在直线![]() 上的坐标平面内是否存在点
上的坐标平面内是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是矩形?若存在,请求出点
为顶点的四边形是矩形?若存在,请求出点![]() 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=![]() x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.
x2+bx+c经过△ABC的三个顶点,其中点A(0,1),点B(﹣9,10),AC∥x轴,点P时直线AC下方抛物线上的动点.

(1)求抛物线的解析式;(2)过点P且与y轴平行的直线l与直线AB、AC分别交于点E、F,当四边形AECP的面积最大时,求点P的坐标;
(3)当点P为抛物线的顶点时,在直线AC上是否存在点Q,使得以C、P、Q为顶点的三角形与△ABC相似,若存在,求出点Q的坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
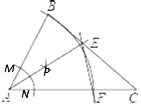
【题目】如图,在△ABC中,∠ABC=2∠C,小明做了如下操作:
(Ⅰ)以A为圆心,AB长为半径画弧,交AC于点F;
(Ⅱ)以A为圆心,任意长为半径画弧,交AB、AC于M、N两点,分别以M、N为圆心,以大于![]() MN为半径画弧,两弧交于一点P,作射线AP,交BC于点E;
MN为半径画弧,两弧交于一点P,作射线AP,交BC于点E;
(Ⅲ)作直线EF.
依据小明尺规作图的方法,若AB=3.3,BE=1.8,则AC的长为___________;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com