
【题目】已知:如图,做![]() 的平分线
的平分线![]() ,在
,在![]() 的两边上分别截取
的两边上分别截取![]() ,再以点
,再以点![]() 为圆心,线段
为圆心,线段![]() 长为半径画弧,交
长为半径画弧,交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:四边形![]() 是菱形;
是菱形;
(2)尺规作图:作线段![]() 的垂直平分线
的垂直平分线![]() ,分别交
,分别交![]() 于点
于点![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() (不写做法,保留作图痕迹);
(不写做法,保留作图痕迹);
(3)当![]() 时,判断
时,判断![]() 的形状,并说明理由.
的形状,并说明理由.
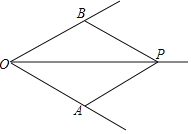
【答案】(1)见解析;(2)见解析;(3)△PBE是直角三角形,见解析.
【解析】
(1)根据四边相等的四边形是菱形即可证明.
(2)利用尺规周长线段OA的垂直平分线即可.
(3)结论:△PBE是直角三角形.想办法证明∠PBE=90°即可.
(1)证明:∵OP是∠AOB的平分线,
∴∠AOP=∠BOP,
∵OA=OB,OP=OP,
∴△AOP≌△BOP(SAS)
∴AP=BP,
∵OA=AP,
∴OA=OB=BP=AP,
∴四边形OAPB是菱形.
(2)解:如图所示.
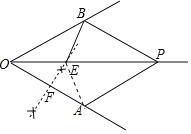
(3)解:结论:△PBE是直角三角形.
理由:连接AE,∵EF是线段OA的垂直平分线,
∴AE=OE,
∵PB=PA,∠EPB=∠EPA,PE=PE,
∴△AEP≌△BEP(SAS),
∴AE=BE,
∴OE=BE,
∴∠BOE=∠OBE,
当∠AOB=60°时,∠BOE=30°,
∴∠OBE=30°,
∵OB=BP,
∴∠BPO=∠BOE=30°,
∴∠OBP=180°-2∠BPO=180°-2×30°=120°,
∴∠PBE=∠OBP-∠OBE=120°-30°=90°,
∴△PBE是直角三角形.


科目:初中数学 来源: 题型:
【题目】(12分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ∶S△ABC=9∶100?若存在,求出t的值;若不存在,说明理由;
(3)当t为何值时,△CPQ为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球有![]() 个,若从中随机摸出一个球,这个球是白球的概率为
个,若从中随机摸出一个球,这个球是白球的概率为![]() .
.
(![]() )请直接写出袋子中白球的个数.
)请直接写出袋子中白球的个数.
(![]() )随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
)随机摸出一个球后,放回并搅匀,再随机摸出一个球,求两次都摸到相同颜色的小球的概率.(请结合树状图或列表解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在多项式的乘法公式中,完全平方公式![]() 是其中重要的一个.
是其中重要的一个.
(1)请补全完全平方公式的推导过程:
![]() ,
,
![]() ,
,
![]() .
.
(2)如图,将边长为![]() 的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
的正方形分割成Ⅰ、Ⅱ、Ⅲ、Ⅳ四部分,请你结合图给出完全平方公式的几何解释.
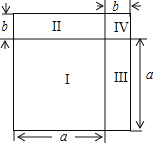
(3)用完全平方公式求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
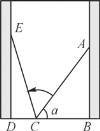
【题目】如图,小巷左右两侧是竖直的墙,一架梯子AC斜靠在右墙,测得梯子顶端距离地面AB=2米,梯子与地面夹角α的正弦值sinα=0.8.梯子底端位置不动,将梯子斜靠在左墙时,顶端距离地面2.4米,则小巷的宽度为( )
A. 0.7米B. 1.5米
C. 2.2米D. 2.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的外接圆,
的外接圆,![]() 为直径,
为直径,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线分别交
的平行线分别交![]() ,
,![]() 的延长线于点
的延长线于点![]() ,
,![]() .
.
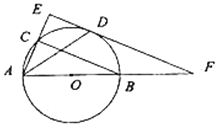
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)设![]() ,
,![]() ,试用含
,试用含![]() ,
,![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(3)若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
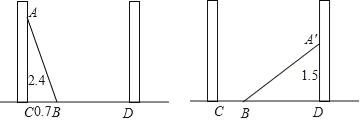
【题目】如图,小巷左石两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A′D为1.5米,求小巷有多宽.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com