
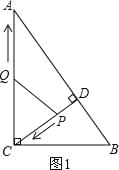
����Ŀ��(12��)��ͼ����Rt��ABC�У���ACB��90����AC��8��BC��6��CD��AB�ڵ�D.��P�ӵ�D���������߶�DC���C�˶�����Q�ӵ�C���������߶�CA���A�˶�������ͬʱ�������ٶȶ�Ϊÿ��1����λ���ȣ�����P�˶���Cʱ�����㶼ֹͣ�����˶�ʱ��Ϊt�룮
(1)������CD�ij���
(2)����CPQ�����ΪS����S��t֮��ĺ�����ϵʽ����ȷ�����˶��������Ƿ����ijһʱ��t��ʹ��S��CPQ��S��ABC��9��100�������ڣ����t��ֵ���������ڣ�˵�����ɣ�
(3)��tΪ��ֵʱ����CPQΪ���������Σ�

���𰸡���1��4��8����2��t=![]() ��t=3����3��t=2��4���
��t=3����3��t=2��4���![]() ���
���![]() �룮
�룮
�������������������1�����ù��ɶ��������AB�������õȻ����Ϳ�����߶�CD�ij���
��2������P��PH��AC������ΪH��ͨ�����������Ƽ�����t�Ĵ���ʽ��ʾPH���Ӷ��������S��t֮��ĺ�����ϵʽ������![]() =9��100����t�ķ��̣��ⷽ�̼��ɽ�����⣮
=9��100����t�ķ��̣��ⷽ�̼��ɽ�����⣮
��3���ɷ���������������ۣ���CQ=CP�ɽ�������t�ķ��̣��Ӷ����t����PQ=PC��QC=QP����ֱ�ӵõ�����t�ķ��̣��ɽ����ڵ��������ε����ߺ�һ�����������ƣ����ɽ�������t�ķ��̣��Ӷ����t��
�����������1����ͼ1���ߡ�ACB=90����AC=8��BC=6��
��AB=10��
��CD��AB��
��S��ABC=![]() BC��AC=
BC��AC=![]() AB��CD��
AB��CD��
��CD=![]() =
=![]() =4.8��
=4.8��
���߶�CD�ij�Ϊ4.8��
��2��������P��PH��AC������ΪH����ͼ2��ʾ��
�����֪DP=t��CQ=t��
��CP=4.8��t��
�ߡ�ACB=��CDB=90����
���HCP=90�㩁��DCB=��B��
��PH��AC��
���CHP=90����
���CHP=��ACB��
���CHP�ס�BCA��
��![]() ��
��
��![]() ��
��
��PH= ![]() ��
��
��![]() =
=![]() CQ��PH=
CQ��PH=![]() t����
t����![]() ��=
��= ![]() ��
��
������ijһʱ��t��ʹ��![]() =9��100��
=9��100��
��![]() =
=![]() ��6��8=24����
��6��8=24����![]() =9��100��
=9��100��
����![]() ����24=9��100��
����24=9��100��
�����ã�5t2��24t+27=0��
����5t��9����t��3��=0��
��ã�t=![]() ��t=3��
��t=3��
��0��t��4.8��
����t=![]() ���t=3��ʱ��
���t=3��ʱ�� ![]() =9��100��
=9��100��
��3������
����CQ=CP����ͼ1��
��t=4.8��t��
��ã�t=2.4��
����PQ=PC����ͼ2��ʾ��
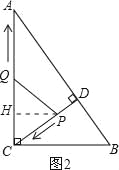
��PQ=PC��PH��QC��
��QH=CH=![]() QC=
QC=![]() ��
��
�ߡ�CHP�ס�BCA��
��![]() ��
��
��![]()
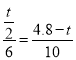 ��
��
��ã�t=![]() ��
��
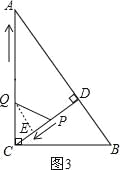
����QC=QP��
����Q��QE��CP������ΪE����ͼ3��ʾ��
ͬ���ɵã�t=![]() ��
��
������������tΪ2.4���![]() ���
���![]() ��ʱ����CPQΪ���������Σ�
��ʱ����CPQΪ���������Σ�


 �ܿ���ȫ��100��ϵ�д�
�ܿ���ȫ��100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ��
��![]() ��
��![]() ��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ���ڣ� ��
��������С����λ�ó������Σ��־���������С��֮����һ�����ﳬ�У�ʹ���е�����С���ľ�����ȣ�����Ӧ���ڣ� ��

A.�ڡ�A����B���ڽ�ƽ���ߵĽ��㴦
B.��AC��BC���ߴ�ֱƽ���ߵĽ��㴦
C.��AC��BC���߸��ߵĽ��㴦
D.��AC��BC�������ߵĽ��㴦
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��AD��BC��D�㣬E��F�ֱ�ΪDB��DC���е㣬��ͼ�й���ȫ�������� �ԣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
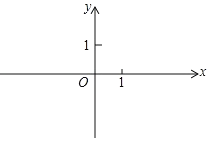
����Ŀ��ֱ��y��2x��2��x�ύ�ڵ�A����y�ύ�ڵ�B��
��1�����A��B�����ꣻ
��2������ֱ��AB��������OAB�������
��3����C��x���ϣ���AC��AB��ֱ��д����C���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016�����)Ϊ��Ч����������Դ����������Ȩ�棬�ҹ����Ϻ��������ȫ����飮��ͼ��һ��������A�����B���ڱ�ƫ��30������C���ڱ�ƫ��15��������100���ﵽ��B������B�����C���ڱ�ƫ��45������B��C������A��C�����ľ��룮(��������������� ![]() ��1.41��
��1.41�� ![]() ��2.45)
��2.45)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̶�����ͬ�����µķ�ѿ���飬������±���ʾ��
ÿ������n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
��ѿ������m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
��ѿ��Ƶ�� | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
�����������ƶϣ�
�ٵ�n=400ʱ���̶���ѿ��Ƶ��Ϊ0.955�������̶���ѿ�ĸ�����0.955��
�ڸ����ϱ��������̶���ѿ�ĸ�����0.95��
����nΪ4000�������̶���ѿ��������ԼΪ3800����
�����ƶϺ������ǣ�������
A. �� B. �٢� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���ʵ��
��1��ʵ��������![]() �У�
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬��
��һ�㣬��![]() ����
����![]() ����ֱ��
����ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����ͼ�٣�ͼ�ڣ�ͼ����ʾ����
����ͼ�٣�ͼ�ڣ�ͼ����ʾ����![]() ����״Ϊ______.
����״Ϊ______.
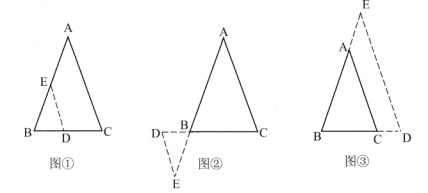
��2����������������������һ������������Σ�����ȫ�������ε����֪ʶ�����һ��������.��ͼ�ܣ�![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ��
��![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() .
.
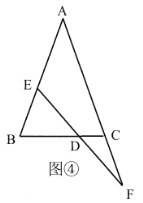
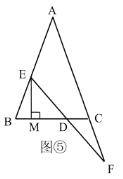
��3����չ��Ӧ��,�ڣ�2���������£���ͼ�ݣ�����![]() ��
��![]() �Ĵ��ߣ�����Ϊ
�Ĵ��ߣ�����Ϊ![]() ����
����![]() ����
����![]() �ij�Ϊ______.
�ij�Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
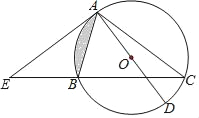
����Ŀ����ͼ����ABC�ڽ��ڡ�O��AD�ǡ�Oֱ����E��CB�ӳ�����һ�㣬�ҡ�BAE=��C��
��1����֤��ֱ��AE�ǡ�O�����ߣ�
��2������BAE=30�㣬��O�İ뾶Ϊ2������Ӱ���ֵ������
��3����EB=AB��cos��E=![]() ��AE=24����EB�ij�����O�İ뾶��
��AE=24����EB�ij�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=ax2+bx+c����A��0��2����
��1�����㣨��![]() ��0��Ҳ�ڸ��������ϣ���a��b����Ĺ�ϵʽ��
��0��Ҳ�ڸ��������ϣ���a��b����Ĺ�ϵʽ��
��2�����������������ⲻͬ����M��x1��y1����N��x2��y2�������㣺��x1��x2��0ʱ����x1��x2����y1��y2����0����0��x1��x2ʱ����x1��x2����y1��y2����0����ԭ��OΪ�ģ�OAΪ�뾶��Բ�뒁���ߵ�����������ΪB��C������ABC��һ���ڽ�Ϊ60�㣮
���������ߵĽ���ʽ��
������P���O���ڵ�A�Գƣ���O��M��N���㹲�ߣ���֤��PAƽ����MPN��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com