练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】绿豆在相同条件下的发芽试验，结果如下表所示：

    每批粒数n

    100

    300

    400

    600

    1000

    2000

    3000

    发芽的粒数m

    96

    282

    382

    570

    948

    1904

    2850

    发芽的频率

    0.960

    0.940

    0.955

    0.950

    0.948

    0.952

    0.950

    下面有三个推断：

    ①当n=400时，绿豆发芽的频率为0.955，所以绿豆发芽的概率是0.955；

    ②根据上表，估计绿豆发芽的概率是0.95；

    ③若n为4000，估计绿豆发芽的粒数大约为3800粒．

    其中推断合理的是（　　）

    A. ① B. ①② C. ①③ D. ②③

    【答案】D

    【解析】

    根据频率估算出概率，利用概率公式逐一判断即可.

    当n=400时，绿豆发芽的频率为0.955，绿豆发芽的概率不一定是0.955，需要大量反复试验，故①不合理；

    随着每批粒数的增加，绿豆发芽的频率总在0.950附近摆动，显示出一定的稳定性，可以估计绿豆发芽的概率是0.950，故②合理；

    根据概率为0.950，若n为4000，估计绿豆发芽的粒数大约为3800粒．故③合理，

    故选D.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线经过A（﹣1，0），B（5，0），C（0，）三点．

    （1）求抛物线的解析式；

    （2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标；

    （3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC，△ADE中，∠BAC＝∠DAE＝90°，AB＝AC，AD＝AE，点C，D，E三点在同一直线上.

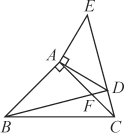
    （1）求证：△BAD≌△CAE；

    （2）猜想BD，CE有何特殊位置关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以点O为圆心，AB长为直径作圆，在⊙O上取一点C，延长AB至点D，连接DC，过点A作⊙O的切线交DC的延长线于点E，且∠DCB＝∠DAC.

    (1)求证：CD是⊙O的切线；

    (2)若AD＝6，tan∠DCB＝，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(12分)如图，在Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，CD⊥AB于点D.点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

    (1)求线段CD的长；

    (2)设△CPQ的面积为S，求S与t之间的函数关系式，并确定在运动过程中是否存在某一时刻t，使得S△CPQ∶S△ABC＝9∶100？若存在，求出t的值；若不存在，说明理由；

    (3)当t为何值时，△CPQ为等腰三角形？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】盒中有若干枚黑棋和白棋，这些棋除颜色外无其他差别，现让学生进行摸棋试验：每次摸出一枚棋，记录颜色后放回摇匀，重复进行这样的试验得到以下数据：

    摸棋的次数n

    100

    200

    300

    500

    800

    1000

    摸到黑棋的次数m

    24

    51

    76

    b

    201

    250

    摸到黑棋的频率（精确到0.001）

    0.240

    a

    0.253

    0.248

    0.251

    0.250

    （1）填空：a=　 　，b=　 　；

    （2）在图中，画出摸到黑棋的折线统计图；

    （3）随机摸一次，估计摸到黑棋的概率．（精确到0.01）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东西方向的海岸线l上有一长为1km的码头MN（如图），在码头西端M的正西19.5km处有一观察站A．某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°，且与A相距40km的B处；经过1小时20分钟，又测得该轮船位于A的北偏东60°，且与A相距km的C处．

    （1）求该轮船航行的速度（保留精确结果）；

    （2）如果该轮船不改变航向继续航行，那么轮船能否正好行至码头MN靠岸？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，以的边为边,向外作等边和等边三角形,连接相交于点.

    (1)求证:;

    (2)求的度数;

    (3)请直接写出的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系，跨度AB=44米，∠A=45°，AC1=4米，点D2的坐标为(-13，-1.69)，则桥架的拱高OH=________米.

    查看答案和解析>>

    同步练习册答案