
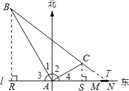
����Ŀ���ڶ�������ĺ�����l����һ��Ϊ1km����ͷMN����ͼ��������ͷ����M������19.5km����һ�۲�վA��ijʱ�̲��һ������ֱ�ߺ��е��ִ�λ��A�ı�ƫ��30��������A���40km��B��������1Сʱ20���ӣ��ֲ�ø��ִ�λ��A�ı�ƫ��60��������A���![]() km��C����
km��C����
��1������ִ����е��ٶȣ�������ȷ�������
��2��������ִ����ı亽��������У���ô�ִ��ܷ�����������ͷMN��������˵�����ɣ�

���𰸡���1��12![]() ��ǧ��/Сʱ������2�����ִ��ܹ�����������ͷMN������
��ǧ��/Сʱ������2�����ִ��ܹ�����������ͷMN������
�������������������1�����ݡ�1=30�㣬��2=60������֪��ABCΪֱ�������Σ����ݹ��ɶ������
��2���ӳ�BC��l��T���Ƚ�AT��AM��AN�Ĵ�С���ɵó����ۣ�
�����������1���ߡ�1=30�㣬��2=60�㣬
���ABCΪֱ�������Σ�
��AB=40km��AC=![]() km��
km��
��BC=![]() ��km����
��km����
��1Сʱ20����=80���ӣ�1Сʱ=60���ӣ�
��![]() ��60=12
��60=12![]() ��ǧ��/Сʱ����
��ǧ��/Сʱ����
��2���ܣ�
���ɣ����߶�BR��AN��R�����߶�CS��AN��S���ӳ�BC��l��T��
�ߡ�2=60�㣬
���4=90�㩁60��=30�㣮
��AC=8![]() ��km����
��km����
��CS=8![]() sin30��=4
sin30��=4![]() ��km����
��km����
��AS=8![]() cos30��=8
cos30��=8![]() ��
��![]() =12��km����
=12��km����
�֡ߡ�1=30�㣬
���3=90�㩁30��=60�㣮
��AB=40km��
��BR=40sin60��=20![]() ��km����
��km����
��AR=40��cos60��=40��![]() =20��km����
=20��km����
�ã���STC�ס�RTB��
����![]() ��
��
![]() .
.
��ã�ST=8��km����
����AT=12+8=20��km����
����ΪAM=19.5km��MN��Ϊ1km����AN=20.5km��
��19.5��AT��20.5
���ִ��ܹ�����������ͷMN������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ������Ϸ��������Ϸ�����˫����ƽ���ǣ�������

A. ��һ��װ��2�������3������ÿ�������ɫ�ⶼ��ͬ���Ĵ�����������һ�����������ʤ�����������һ�ʤ��
B. �ӱ��к���1��100��100�ſ�Ƭ�У������ȡһ�ţ��鵽����Ϊ������ʤ�������һ�ʤ��
C. ������һö�ʵؾ��ȵ����ӣ������ĵ���С��4���ʤ�������ĵ�������4���һ�ʤ��
D. ��С������ͼ��ʾ�ĵذ������ɵع������������ͣ��ij�鷽���ϣ���С��ͣ�ں�ɫ�������ʤ����ͣ�ڰ�ɫ�������һ�ʤ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
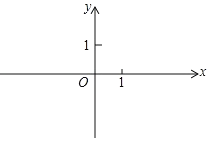
����Ŀ��ֱ��y��2x��2��x�ύ�ڵ�A����y�ύ�ڵ�B��
��1�����A��B�����ꣻ
��2������ֱ��AB��������OAB�������
��3����C��x���ϣ���AC��AB��ֱ��д����C���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���̶�����ͬ�����µķ�ѿ���飬������±���ʾ��
ÿ������n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
��ѿ������m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
��ѿ��Ƶ�� | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
�����������ƶϣ�
�ٵ�n=400ʱ���̶���ѿ��Ƶ��Ϊ0.955�������̶���ѿ�ĸ�����0.955��
�ڸ����ϱ��������̶���ѿ�ĸ�����0.95��
����nΪ4000�������̶���ѿ��������ԼΪ3800����
�����ƶϺ������ǣ�������
A. �� B. �٢� C. �٢� D. �ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
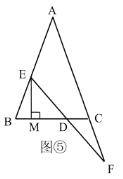
����Ŀ���ۺ���ʵ��
��1��ʵ��������![]() �У�
��![]() ��
��![]() Ϊֱ��
Ϊֱ��![]() ��һ�㣬��
��һ�㣬��![]() ����
����![]() ����ֱ��
����ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ����ͼ�٣�ͼ�ڣ�ͼ����ʾ����
����ͼ�٣�ͼ�ڣ�ͼ����ʾ����![]() ����״Ϊ______.
����״Ϊ______.
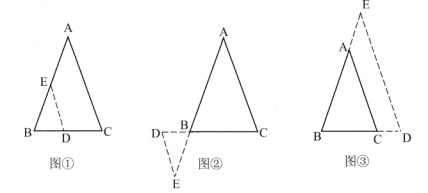
��2����������������������һ������������Σ�����ȫ�������ε����֪ʶ�����һ��������.��ͼ�ܣ�![]() �У�
��![]() ��
��![]() Ϊ
Ϊ![]() ��һ�㣬
��һ�㣬![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬��
�ӳ�����һ�㣬��![]() ��
��![]() ��
��![]() ��
��![]() ����֤��
����֤��![]() .
.
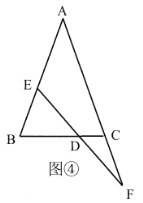
��3����չ��Ӧ��,�ڣ�2���������£���ͼ�ݣ�����![]() ��
��![]() �Ĵ��ߣ�����Ϊ
�Ĵ��ߣ�����Ϊ![]() ����
����![]() ����
����![]() �ij�Ϊ______.
�ij�Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ AB=AC��CD��AB��D��BE��AC��E��BE��CD�ཻ�ڵ�O��
��1����֤AD=AE��
��2������OA��BC�����ж�ֱ��OA��BC�Ĺ�ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
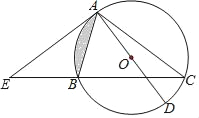
����Ŀ����ͼ����ABC�ڽ��ڡ�O��AD�ǡ�Oֱ����E��CB�ӳ�����һ�㣬�ҡ�BAE=��C��
��1����֤��ֱ��AE�ǡ�O�����ߣ�
��2������BAE=30�㣬��O�İ뾶Ϊ2������Ӱ���ֵ������
��3����EB=AB��cos��E=![]() ��AE=24����EB�ij�����O�İ뾶��
��AE=24����EB�ij�����O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����������y=kx��k��0����ͼ����x���ཻ���ɵ����Ϊ70�㣬����A������Ϊ��0��8����PΪy���ϵ�һ�����㣬M��NΪ����y=kx��k��0����ͼ���ϵ��������㣬��AM+MP+PN����СֵΪ��������
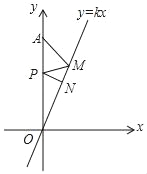
A. 4 B. 4![]() C. 8sin40�� D. 8sin20�㣨1+cos20��+sin20��cos20�㣩
C. 8sin40�� D. 8sin20�㣨1+cos20��+sin20��cos20�㣩
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ�ҹ������˱Ƚ����Ƶľ�������ѧ��������ϵ��ijУȥ���ϰ��귢�Ÿ�ÿ����������ѧ��389Ԫ�������ϰ��귢����438Ԫ����ÿ���귢�ŵ���������ƽ��������Ϊ![]() ���������г��ķ�������ȷ���ǣ� ��
���������г��ķ�������ȷ���ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com