
【题目】如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,8),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
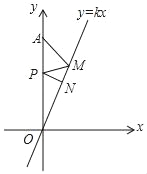
A. 4 B. 4![]() C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一直线上.
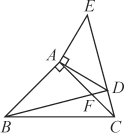
(1)求证:△BAD≌△CAE;
(2)猜想BD,CE有何特殊位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在东西方向的海岸线l上有一长为1km的码头MN(如图),在码头西端M的正西19.5km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距![]() km的C处.
km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
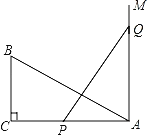
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠BAC=90°,∠B=45°,O为BC中点,如果点M、N分别在线段AB、AC上移动,设AM长为x,CN的长为y,且x、y满足等式![]() =0(a>0).
=0(a>0).
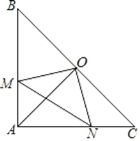
(1)求证:BM=AN;
(2)请你证明△OMN为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得△AB′C′,即如图①,我们将这种变换记为[θ,n].
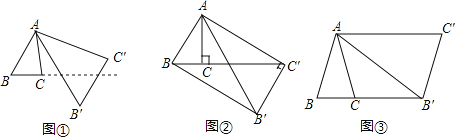
(1)如图①,对△ABC作变换[60°,![]() ]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
]得△AB′C′,则S△AB′C′:S△ABC= ;直线BC与直线B′C′所夹的锐角为 度;
(2)如图②,△ABC中,∠BAC=30°,∠ACB=90°,对△ABC 作变换[θ,n]得△AB'C',使点B、C、C′在同一直线上,且四边形ABB'C'为矩形,求θ和n的值;
(3)如图③,△ABC中,AB=AC,∠BAC=36°,BC=l,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB'C'为平行四边形,求θ和n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个拱形桥架可以近似看作是由等腰梯形ABD8D1和其上方的抛物线D1OD8组成.若建立如图所示的直角坐标系,跨度AB=44米,∠A=45°,AC1=4米,点D2的坐标为(-13,-1.69),则桥架的拱高OH=________米.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标是(20,0),点B的坐标是(16,0),点C、D在以OA为直径的半圆M上,且四边形OCDB是平行四边形,则点C的坐标为______.
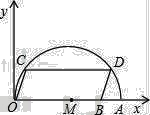
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com