
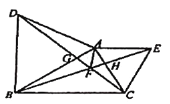
【题目】如图,以![]() 的边
的边![]() 为边,向外作等边
为边,向外作等边![]() 和等边三角形
和等边三角形![]() ,连接
,连接![]() 相交于点
相交于点![]() .
.
(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)请直接写出![]() 的度数.
的度数.
【答案】(1)证明见解析;(2) 120![]() ;(3) 60
;(3) 60![]()
【解析】
(1)由三角形ABD与三角形ACE都为等边三角形,利用等边三角形的性质得到两组对应边相等,两三角形的内角都为60°,利用等式的性质得到∠DAC=∠BAE,利用SAS可得出△DAC≌△BAE,得证;
(2)由△DAC≌△BAE,利用全等三角形的对应角相等得到∠ACD=∠AEB,而∠DFE为三角形EFC的外角,利用外角的性质列出关系式,等量代换后即可求出其度数.
(3)作AM⊥BE,AN⊥DC,利用全等三角形及面积法证得AM=AN,点A在∠DFE的平分线上,从而求得结论.
(1)∵△ABD和△ACE都为等边三角形,
∴AD=AB,AE=AC,∠DAB=∠EAC=∠AEC=∠ACE=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,
在△DAC和△BAE中,
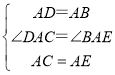
∴△DAC≌△BAE(SAS)
∴![]() ;
;
(2)由(1)中△DAC≌△BAE得:![]()
∵∠DFE为三角形EFC的外角,
∴∠DFE=∠FCE+∠CEF=∠FCA+∠ACE+∠CEF=∠ACE+∠CEF+∠FEA=∠ACE+∠AEC=60![]() =120
=120![]() ;
;
(3)过点A分别作AM⊥BE,AN⊥DC,垂足为点M,N.
∵由(1)知:△DAC≌△BAE,
∴![]() =
=![]() ,
,![]()
∴![]() DCAN=
DCAN=![]() BEAM
BEAM
∴AM=AN
∴点A在∠DFE的平分线上,
即FA平分∠DFE
∴∠AFD=![]() ∠DFE=60
∠DFE=60![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我市某蔬菜生产基地用装有恒温系统的大棚栽培一种适宜生长温度为15﹣20℃的新品种,如图是某天恒温系统从开启到关闭及关闭后,大棚里温度y(℃)随时间x(h)变化的函数图象,其中AB段是恒温阶段,BC段是双曲线![]() 的一部分,请根据图中信息解答下列问题:
的一部分,请根据图中信息解答下列问题:
(1)求k的值;
(2)恒温系统在一天内保持大棚里温度在15℃及15℃以上的时间有多少小时?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿豆在相同条件下的发芽试验,结果如下表所示:
每批粒数n | 100 | 300 | 400 | 600 | 1000 | 2000 | 3000 |
发芽的粒数m | 96 | 282 | 382 | 570 | 948 | 1904 | 2850 |
发芽的频率 | 0.960 | 0.940 | 0.955 | 0.950 | 0.948 | 0.952 | 0.950 |
下面有三个推断:
①当n=400时,绿豆发芽的频率为0.955,所以绿豆发芽的概率是0.955;
②根据上表,估计绿豆发芽的概率是0.95;
③若n为4000,估计绿豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A. ① B. ①② C. ①③ D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;
(2)连接OA,BC,试判断直线OA,BC的关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
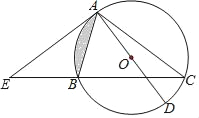
【题目】如图,△ABC内接于⊙O,AD是⊙O直径,E是CB延长线上一点,且∠BAE=∠C.
(1)求证:直线AE是⊙O的切线;
(2)若∠BAE=30°,⊙O的半径为2,求阴影部分的面积;
(3)若EB=AB,cos∠E=![]() ,AE=24,求EB的长及⊙O的半径.
,AE=24,求EB的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,8),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
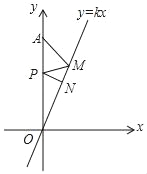
A. 4 B. 4![]() C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
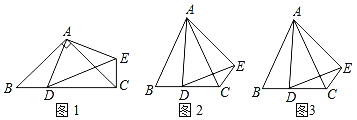
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=_____度;如图2,当点D在线段BC上,如果∠BAC=60°,则∠BCE=______度.
(2)设∠BAC=α,∠BCE=β,如图3,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com