
【题目】无论![]() 取什么实数时,点P
取什么实数时,点P![]() 总在直线
总在直线![]() 上,且点
上,且点![]() 也在直线
也在直线![]() 上,则
上,则![]() 的值为__________.
的值为__________.
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
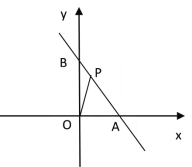
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
(1)填空:a= ,b= ;
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)
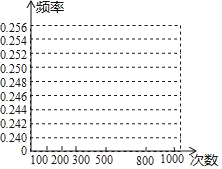
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在Rt△ABC中,∠BAC=90°,∠B=45°,O为BC中点,如果点M、N分别在线段AB、AC上移动,设AM长为x,CN的长为y,且x、y满足等式![]() =0(a>0).
=0(a>0).
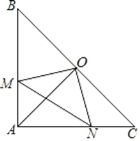
(1)求证:BM=AN;
(2)请你证明△OMN为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是△ABC的外接圆,且AB=BC=CD,AB∥CD,连接BD.
(1)求证:BD是⊙O的切线;
(2)若AB=10,cos∠BAC=![]() ,求BD的长及⊙O的半径.
,求BD的长及⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射击队为了解运动员的年龄情况,作了一次年龄调查,根据射击运动员的年龄(单位:岁),绘制出如图的统计图.
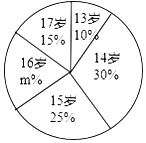
(1)求m的值;
(2)该射击队运动员年龄是众数是 .
(3)求该射击队运动员的平均年龄;
(4)若该射击队有13岁运动员2人,则该射击队中14岁运动员有几人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com