
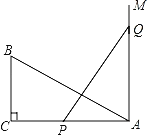
【题目】如图,在直角三角形ABC中,∠C=90°,AC=20,BC=10,PQ=AB,P,Q两点分别在线段AC和过点A且垂直于AC的射线AM上运动,且点P不与点A,C重合,那么当点P运动到什么位置时,才能使△ABC与△APQ全等?
 字词句段篇系列答案
字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】综合与实践
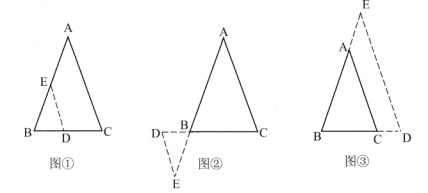
(1)实践操作:![]() 中,
中,![]() ,
,![]() 为直线
为直线![]() 上一点,过
上一点,过![]() 点作
点作![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,如图①,图②,图③所示,则
,如图①,图②,图③所示,则![]() 的形状为______.
的形状为______.
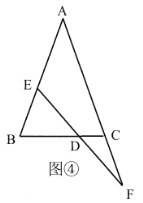
(2)问题解决:等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起解决问题.如图④,![]() 中,
中,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() ,
,![]() 交
交![]() 于
于![]() ,求证:
,求证:![]() .
.
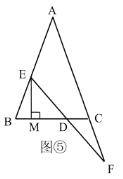
(3)拓展与应用,在(2)的条件下,如图⑤,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,若
,若![]() ,则
,则![]() 的长为______.
的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
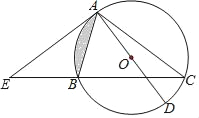
【题目】如图,△ABC内接于⊙O,AD是⊙O直径,E是CB延长线上一点,且∠BAE=∠C.
(1)求证:直线AE是⊙O的切线;
(2)若∠BAE=30°,⊙O的半径为2,求阴影部分的面积;
(3)若EB=AB,cos∠E=![]() ,AE=24,求EB的长及⊙O的半径.
,AE=24,求EB的长及⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )

A. 点F B. 点E C. 点A D. 点C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=kx(k>0)的图象与x轴相交所成的锐角为70°,定点A的坐标为(0,8),P为y轴上的一个动点,M、N为函数y=kx(k>0)的图象上的两个动点,则AM+MP+PN的最小值为( )
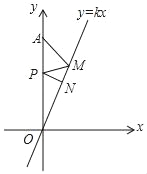
A. 4 B. 4![]() C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
C. 8sin40° D. 8sin20°(1+cos20°+sin20°cos20°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=6,BC=8.点P在矩形ABCD的内部,点E在边BC上,满足△PBE∽△DBC,若△APD是等腰三角形,则PE的长为数___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c过点A(0,2).
(1)若点(﹣![]() ,0)也在该抛物线上,求a,b满足的关系式;
,0)也在该抛物线上,求a,b满足的关系式;
(2)若该抛物线上任意不同两点M(x1,y1),N(x2,y2)都满足:当x1<x2<0时,(x1﹣x2)(y1﹣y2)>0;当0<x1<x2时,(x1﹣x2)(y1﹣y2)<0.以原点O为心,OA为半径的圆与拋物线的另两个交点为B,C,且△ABC有一个内角为60°.
①求抛物线的解析式;
②若点P与点O关于点A对称,且O,M,N三点共线,求证:PA平分∠MPN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com