
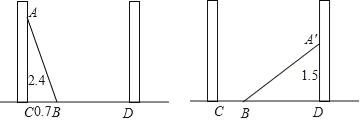
【题目】如图,小巷左石两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离BC为0.7米,梯子顶端到地面的距离AC为2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,梯子顶端到地面的距离A′D为1.5米,求小巷有多宽.
科目:初中数学 来源: 题型:
【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A,C的坐标分别为(﹣4,5),(﹣1,3).

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的△A′B′C′,并写出点B′的坐标;
(3)P是x轴上的动点,在图中找出使△A′BP周长最短时的点P,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个两位数,个位数比十位数大2,若把各位数字和十位数字对调,则所得的新的两位数比原数的两倍少17.若设原数的个位数为![]() ,十位数字为
,十位数字为![]() ,则下列方程组正确的是( )
,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成推理过程
(1)如图,已知∠1=∠2,∠B=∠C,求证:AB∥CD.
证明∵∠1=∠2(已知),
且∠1=∠CGD( )
∴∠2=∠CGD( ),
∴CE∥BF( ),
∴∠C=∠BFD( )
又∵∠B=∠C(已知),
∴∠BFD=∠B( ),
∴AB∥CD( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中.
(1)写出△ABC各顶点的坐标.
(2)把△ABC向上平移2个单位,再向右平移2个单位得△A'B'C',在图中画出△A'B'C',并写出A'、B'、C'的坐标.
(3)求出![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC=45°,AB= ![]() ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 .
,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB、AC于E、F,连接EF,则线段EF长度的最小值为 . 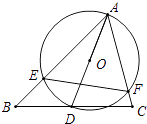
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为6 m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是

A. AB=12 m B. MN∥AB
C. △CMN∽△CAB D. CM∶MA=1∶2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.

(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com