
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析:(1)首先证得△ADE≌△CDE,由全等三角形的性质可得∠ADE=∠CDE,由AD∥BC可得∠ADE=∠CBD,易得∠CDB=∠CBD,可得BC=CD,易得AD=BC,利用平行线的判定定理可得四边形ABCD为平行四边形,由AD=CD可得四边形ABCD是菱形;
(2)由BE=BC可得△BEC为等腰三角形,可得∠BCE=∠BEC,利用三角形的内角和定理可得∠CBE=180×![]() =45°,易得∠ABE=45°,可得∠ABC=90°,由正方形的判定定理可得四边形ABCD是正方形.
=45°,易得∠ABE=45°,可得∠ABC=90°,由正方形的判定定理可得四边形ABCD是正方形.
试题解析:(1)在△ADE与△CDE中,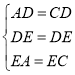 ,∴△ADE≌△CDE,∴∠ADE=∠CDE,
,∴△ADE≌△CDE,∴∠ADE=∠CDE,
∵AD∥BC,∴∠ADE=∠CBD,∴∠CDE=∠CBD,∴BC=CD,
∵AD=CD,∴BC=AD,∴四边形ABCD为平行四边形,
∵AD=CD,∴四边形ABCD是菱形;
(2)∵BE=BC,∴∠BCE=∠BEC,
∵∠CBE:∠BCE=2:3,∴∠CBE=180×![]() =45°,
=45°,
∵四边形ABCD是菱形,∴∠ABE=45°,∴∠ABC=90°,∴四边形ABCD是正方形.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:
【题目】如图,将矩形纸片ABCD沿直线MN折叠,顶点B恰好与CD边上的动点P重合(点P不与点C,D重合),折痕为MN,点M,N分别在边AD,BC上,连接MB,MP,BP,BP与MN相交于点F.
(1)求证:△BFN∽△BCP;
(2)①在图2中,作出经过M,D,P三点的⊙O(要求保留作图痕迹,不写做法);
②设AB=4,随着点P在CD上的运动,若①中的⊙O恰好与BM,BC同时相切,求此时DP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
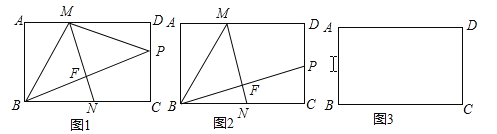
【题目】如图,已知函数y=﹣ ![]() x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
x+b的图象与x轴、y轴分别交于点A、B,与函数y=x的图象交于点M,点M的横坐标为2.
(1)求点A的坐标;
(2)在x轴上有一动点P(a,0)(其中a>2),过点P作x轴的垂线,分别交函数y=﹣ ![]() +b和y=x的图象于点C、D.
+b和y=x的图象于点C、D.
①若OB=2CD,求a的值;
②是否存在这样的点P,使以B、O、C、D为顶点的四边形是平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为5,PA是⊙O的一条切线,切点为A,连接PO并延长,交⊙O于点B,过点A作AC⊥PB交⊙O于点C、交PB于点D,连接BC,当∠P=30°时,
(1)求弦AC的长;
(2)求证:BC∥PA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处,则A′C=cm. 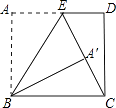
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级某同学6次数学小测验的成绩分别为:80分,85分,95分,95分,95分,100分,则该同学这6次成绩的众数和中位数分别是( )
A.95分,95分
B.95分,90分
C.90分,95分
D.95分,85分
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,弦CD与直径AB相交于点F.点E在⊙O外,做直线AE,且∠EAC=∠D.
(1)求证:直线AE是⊙O的切线.
(2)若∠BAC=30°,BC=4,cos∠BAD=![]() ,CF=
,CF=![]() ,求BF的长.
,求BF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com