
【题目】如图,矩形ABCD中,AB=15cm,点E在AD上,且AE=9cm,连接EC,将矩形ABCD沿直线BE翻折,点A恰好落在EC上的点A′处,则A′C=cm. 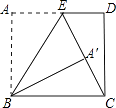
【答案】8
【解析】解:∵四边形ABCD是矩形,
∴AB=CD=15cm,∠A=∠D=90°,AD∥BC,AD=BC,
∴∠DEC=∠A′CB,
由折叠的性质,得:A′B=AB=15cm,∠BA′E=∠A=90°,
∴A′B=CD,∠BA′C=∠D=90°,
在△A′BC和△DCE中,
 ,
,
∴△A′BC≌△DCE(AAS),
∴A′C=DE,
设A′C=xcm,则BC=AD=DE+AE=x+9(cm),
在Rt△A′BC中,BC2=A′B2+A′C2,
即(x+9)2=x2+152,
解得:x=8,
∴A′C=8cm.
所以答案是:8.
【考点精析】掌握翻折变换(折叠问题)是解答本题的根本,需要知道折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在平行四边形ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连接EG、GF、FH、HE.
(1)如图1,试判断四边形EGFH的形状,并说明理由; 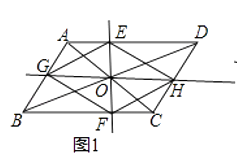
(2)如图2,当EF⊥GH,AC=BD时,四边形EGFH的形状是; 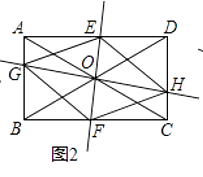
(3)在(2)的条件下,若AC⊥BD(如图3),四边形EGFH的形状是 . 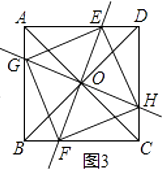
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD中,AD∥BC,AD=CD,E是对角线BD上一点,且EA=EC.
(1)求证:四边形ABCD是菱形;
(2)如果BE=BC,且∠CBE:∠BCE=2:3,求证:四边形ABCD是正方形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的一块地,已知∠ADC=90°,AD=12m,CD=9m,AB=25m,BC=20m,则这块地的面积为( )平方米.
A.96
B.204
C.196
D.304
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com