
【题目】(题文)如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.
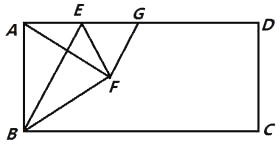
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
【答案】(1)见解析;(2)![]() ;(3)n=16或 8+4
;(3)n=16或 8+4![]() .
.
【解析】试题(1)因为GF⊥AF,由对称易得AE=EF,则由直角三角形的两个锐角的和为90度,且等边对等角,即可证明E是AG的中点;(2)可设AE=a,则AD=na,即需要用n或a表示出AB,由BE⊥AF和∠BAE==∠D=90°,可证明△ABE~△DAC , 则![]() ,因为AB=DC,且DA,AE已知表示出来了,所以可求出AB,即可解答;(3)求以点F,C,G为顶点的三角形是直角三角形时的n,需要分类讨论,一般分三个,∠FCG=90°,∠CFG=90°,∠CGF=90°;根据点F在矩形ABCD的内部就可排除∠FCG=90°,所以就以∠CFG=90°和∠CGF=90°进行分析解答.
,因为AB=DC,且DA,AE已知表示出来了,所以可求出AB,即可解答;(3)求以点F,C,G为顶点的三角形是直角三角形时的n,需要分类讨论,一般分三个,∠FCG=90°,∠CFG=90°,∠CGF=90°;根据点F在矩形ABCD的内部就可排除∠FCG=90°,所以就以∠CFG=90°和∠CGF=90°进行分析解答.
试题解析:(1)证明:由对称得AE=FE,∴∠EAF=∠EFA,∵GF⊥AE,∴∠EAF+∠FGA=∠EFA+∠EFG=90°,∴∠FGA=∠EFG,∴EG=EF,∴AE=EG.
(2)解:设AE=a,则AD=na,当点F落在AC上时(如图1),由对称得BE⊥AF,∴∠ABE+∠BAC=90°,∵∠DAC+∠BAC=90°,∴∠ABE=∠DAC,又∵∠BAE=∠D=90°,∴△ABE~△DAC ,∴![]()
∵AB=DC,∴AB2=AD·AE=na·a=na2,∵AB>0,∴AB=![]() ,∴
,∴![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() .
.
(3)解:设AE=a,则AD=na,由AD=4AB,则AB=![]() .
.
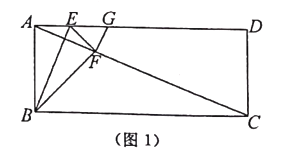
当点F落在线段BC上时(如图2),EF=AE=AB=a,此时![]() ,∴n=4,∴当点F落在矩形外部时,n>4.
,∴n=4,∴当点F落在矩形外部时,n>4.
∵点F落在矩形的内部,点G在AD上,∴∠FCG<∠BCD,∴∠FCG<90°,若∠CFG=90°,则点F落在AC上,由(2)得![]() =
=![]() ,∴n=16.
,∴n=16.
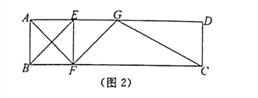
若∠CGF=90°(如图3),则∠CGD+∠AGF=90°,∵∠FAG+∠AGF=90°,∴∠CGD=∠FAG=∠ABE,∵∠BAE=∠D=90°,∴△ABE~△DGC,∴ ![]() ,∴AB·DC=DG·AE,即
,∴AB·DC=DG·AE,即![]() .
.
解得 n=![]() 或n=
或n=![]() <4(不合题意,舍去),∴当n=16或
<4(不合题意,舍去),∴当n=16或 ![]() 时,以点F,C,G为顶点的三角形是直角三角形.
时,以点F,C,G为顶点的三角形是直角三角形.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
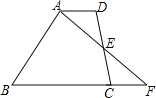
【题目】如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)求证:CF=AD.
(2)若AD=3,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
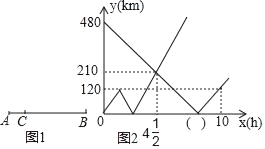
【题目】如图1所示,在A,B两地之间有汽车站C站,客车由C站驶往A地,到达A地后立即原速驶往B地,货车由B地驶往A地,两车同时出发,匀速行驶.图2是客车、货车离C站的距离y(千米)与行驶时间x(小时)之间的函数关系图象,请结合图象信息解答下列问题:
(1)A,B两地间的距离是 千米;请直接在图2中的括号内填上正确数字;
(2)求货车由B地驶往A地过程中,y与x之间的函数关系式,并写出自变量x的取值范围;
(3)客、货两车出发多长时间,距各自出发地的距离相等?直接写出答案;
(4)客、货两车出发多长时间,相距500千米?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件数如下:
每人加工零件数 | 540 | 450 | 300 | 240 | 210 | 120 |
人数 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)写出这15人该月加工零件的平均数、中位数和众数;
(2)生产部负责人要定出合理的每人每月生产定额,你认为应该定为多少件合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,点P是对角线AC上的一点,PE⊥AB,PF⊥AD,垂足分别为E、F,且PE=PF,平行四边形ABCD是菱形吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=AD=6,AB⊥BC,AD⊥CD,∠BAD=60°,点M、N分别在AB、AD边上,若AM:MB=AN:ND=1:2,则tan∠MCN=

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com