
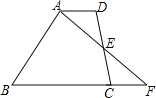
【题目】如图,在梯形ABCD中,AD∥BC,E为CD中点,连接AE并延长AE交BC的延长线于点F.
(1)求证:CF=AD.
(2)若AD=3,AB=8,当BC为多少时,点B在线段AF的垂直平分线上,为什么?
【答案】(1)见解析;(2)当BC=5时,点B在线段AF的垂直平分线上,理由见解析.
【解析】
(1)根据平行线的性质可得∠D=∠ECF,利用ASA可证明△FEC≌△AED,即可证明CF=AD;
(2)若点B在线段AF的垂直平分线上,则应有AB=BF,根据AB=8,CF=AD=3,BC=BF﹣CF即可求出BC的长.
(1)∵AD∥BC,
∴∠D=∠DCF,
在△FEC与△AED中, ,
,
∴△FEC≌△AED(ASA),
∴CF=AD.
(2)当BC=5时,点B在线段AF的垂直平分线上,
理由:∵点B在AF的垂直平分线上,
∴AB=BF,
∴AB=BC+CF,
∵AD=CF,
∴AB=BC+AD,
∵BC=5,AD=3,AB=8,
∴BC=AB-AD=5,
∴当BC=5时,点B在线段AF的垂直平分线上.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案科目:初中数学 来源: 题型:
【题目】阅读与思考:整式乘法与因式分解是方向相反的变形,由(x+p)(x+q)=x2+(p+q)x+pq得,x2+(p+q)x+pq=(x+p)(x+q);利用这个式子可以将某些二次项系数是1的二次三项式分解因式,例如:将式子x2﹣x﹣6分解因式.这个式子的常数项﹣6=2×(﹣3),一次项系数﹣1=2+(﹣3),这个过程可用十字相乘的形式形象地表示:先分解常数项,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数.如图所示.这种分解二次三项式的方法叫“十字相乘法”,请同学们认真观察,分析理解后,解答下列问题.
(1)分解因式:x2+7x﹣18.
(2)填空:若x2+px﹣8可分解为两个一次因式的积,则整数p的所有可能值是 .
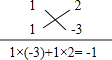
查看答案和解析>>
科目:初中数学 来源: 题型:
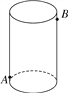
【题目】如图,圆柱形玻璃容器高19cm,底面周长为60cm,在外侧距下底1.5cm的点A处有一只蜘蛛,在蜘蛛正对面的圆柱形容器的外侧,距上底1.5cm处的点B处有一只苍蝇,蜘蛛急于捕捉苍蝇充饥,请你帮蜘蛛计算它沿容器侧面爬行的最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
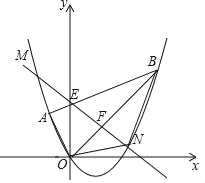
【题目】如图,平面直角坐标系xOy中点A的坐标为(﹣1,1),点B的坐标为(3,3),抛物线经过A、O、B三点,连接OA、OB、AB,线段AB交y轴于点E.
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连接ON、BN,当四边形ABNO的面积最大时,求点N的坐标并求出四边形ABNO面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,对称轴为直线x=1的抛物线y=﹣x2+bx+c与x轴交于点A和点B,与y轴交于点C,且点B的坐标为(﹣1,0)
(1)求抛物线的解析式并作出图象;
(2)点D的坐标为(0,1),点P是抛物线上的动点,若△PCD是以CD为底的等腰三角形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市今年中考理化实验操作考试,采用学生抽签方式决定自己的考试内容.规定:每位考生必须在三个物理实验(用纸签A、B、C表示)和三个化学实验(用纸签D、E、F表示)中各抽取一个进行考试,小刚在看不到纸签的情况下,分别从中各随机抽取一个.
(1) 用“列表法”或“树状图法”表示所有可能出现的结果;
(2) 小刚抽到物理实验B和化学实验F(记作事件P)的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(题文)如图,在矩形ABCD中,点E是AD上的一个动点,连接BE,作点A关于BE的对称点F,且点F落在矩形ABCD的内部,连结AF,BF,EF,过点F作GF⊥AF交AD于点G,设 ![]() =n.
=n.
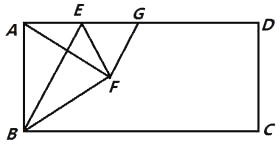
(1)求证:AE=GE;
(2)当点F落在AC上时,用含n的代数式表示![]() 的值;
的值;
(3)若AD=4AB,且以点F,C,G为顶点的三角形是直角三角形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF中,AB=DE,∠B=∠DEF.
(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添加的条件是 ;
(2)添加了条件后,证明△ABC≌△EFD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com