
【题目】如图,抛物线y=﹣x2+bx+c与直线y= ![]() x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3,
x+2交于C、D两点,其中点C在y轴上,点D的坐标为(3, ![]() ).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.
).点P是y轴右侧的抛物线上一动点,过点P作PE⊥x轴于点E,交CD于点F.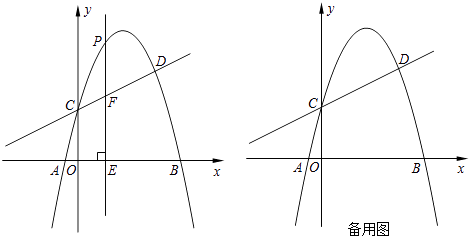
(1)求抛物线的解析式;
(2)若点P的横坐标为m,当m为何值时,以O、C、P、F为顶点的四边形是平行四边形?请说明理由.
(3)若存在点P,使∠PCF=45°,请直接写出相应的点P的坐标.
【答案】
(1)
解:在直线解析式y= ![]() x+2中,令x=0,得y=2,
x+2中,令x=0,得y=2,
∴C(0,2).
∵点C(0,2)、D(3, ![]() )在抛物线y=﹣x2+bx+c上,
)在抛物线y=﹣x2+bx+c上,
∴ 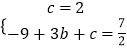 ,
,
解得b= ![]() ,c=2,
,c=2,
∴抛物线的解析式为:y=﹣x2+ ![]() x+2
x+2
(2)
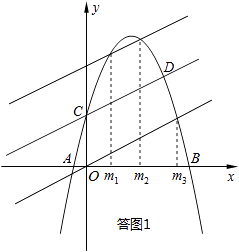
解:∵PF∥OC,且以O、C、P、F为顶点的四边形是平行四边形,
∴PF=OC=2,
∴将直线y= ![]() x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
x+2沿y轴向上、下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.
由答图1可以直观地看出,这样的交点有3个.
将直线y= ![]() x+2沿y轴向上平移2个单位,得到直线y=
x+2沿y轴向上平移2个单位,得到直线y= ![]() x+4,
x+4,
联立  ,
,
解得x1=1,x2=2,
∴m1=1,m2=2;
将直线y= ![]() x+2沿y轴向下平移2个单位,得到直线y=
x+2沿y轴向下平移2个单位,得到直线y= ![]() x,
x,
联立  ,
,
解得x3= ![]() ,x4=
,x4= ![]() (在y轴左侧,不合题意,舍去),
(在y轴左侧,不合题意,舍去),
∴m3= ![]() .
.
∴当m为值为1,2或 ![]() 时,以O、C、P、F为顶点的四边形是平行四边形
时,以O、C、P、F为顶点的四边形是平行四边形
(3)
解:存在.
理由:设点P的横坐标为m,则P(m,﹣m2+ ![]() m+2),F(m,
m+2),F(m, ![]() m+2).
m+2).
如答图2所示,过点C作CM⊥PE于点M,则CM=m,EM=2,
∴FM=yF﹣EM= ![]() m,
m,
∴tan∠CFM=2.
在Rt△CFM中,由勾股定理得:CF= ![]() m.
m.
过点P作PN⊥CD于点N,
则PN=FNtan∠PFN=FNtan∠CFM=2FN.
∵∠PCF=45°,
∴PN=CN,
而PN=2FN,
∴FN=CF= ![]() m,PN=2FN=
m,PN=2FN= ![]() m,
m,
在Rt△PFN中,由勾股定理得:PF= ![]() =
= ![]() m.
m.
∵PF=yP﹣yF=(﹣m2+ ![]() m+2)﹣(
m+2)﹣( ![]() m+2)=﹣m2+3m,
m+2)=﹣m2+3m,
∴﹣m2+3m= ![]() m,
m,
整理得:m2﹣ ![]() m=0,
m=0,
解得m=0(舍去)或m= ![]() ,
,
∴P( ![]() ,
, ![]() );
);
同理求得,另一点为P( ![]() ,
, ![]() ).
).
∴符合条件的点P的坐标为( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ).
).
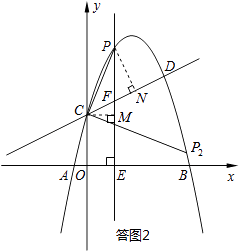
【解析】(1)首先求出点C的坐标,然后利用待定系数法求出抛物线的解析式;(2)本问采用数形结合的数学思想求解.将直线y= ![]() x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标.
x+2沿y轴向上或向下平移2个单位之后得到的直线,与抛物线y轴右侧的交点,即为所求之交点.由答图1可以直观地看出,这样的交点有3个.联立解析式解方程组,即可求出m的值;(3)本问符合条件的点P有2个,如答图2所示,注意不要漏解.在求点P坐标的时候,需要充分挖掘已知条件,构造直角三角形或相似三角形,解方程求出点P的坐标.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】某学习小组在学习了函数及函数图象的知识后,想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
(1)列函数表达式:若矩形的周长为8,设矩形的一边长为x,面积为y,则有y=____________;
(2)上述函数表达式中,自变量x的取值范围是____________;
(3)列表:
x | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y | … | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | … |
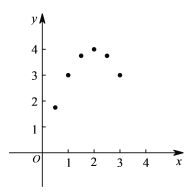
写出m=____________;
(4)画图:在平面直角坐标系中已描出了上表中部分各对应值为坐标的点,请你画出该函数的图象;
(5)结合图象可得,x=____________时,矩形的面积最大;写出该函数的其它性质(一条即可):____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm.射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s). 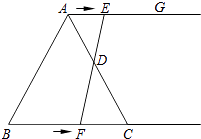
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)填空: ①当t为s时,四边形ACFE是菱形;
②当t为s时,以A、F、C、E为顶点的四边形是直角梯形.
查看答案和解析>>
科目:初中数学 来源: 题型:
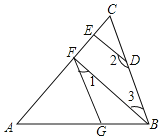
【题目】如图,![]() 于点E,
于点E,![]() 于点F,
于点F,![]() ,求证:
,求证:![]() .
.
试将下面的证明过程补充完整![]() 填空
填空![]() :
:
证明:![]() ,
,![]() 已知
已知![]()
![]() ______
______![]()
![]() 同位角相等,两直线平行
同位角相等,两直线平行![]() ,
,
![]() 两直线平行,同旁内角互补
两直线平行,同旁内角互补![]() ,
,
又![]() 已知
已知![]() ,
,
![]() ______,
______,![]() 同角的补角相等
同角的补角相等![]()
![]() ______
______![]() 内错角相等,两直线平行
内错角相等,两直线平行![]() ,
,
![]() ______
______![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,菱形ABCD的顶点A的坐标为![]() ,点B的坐标为
,点B的坐标为![]() ,点C在第一象限,对角线BD与x轴平行
,点C在第一象限,对角线BD与x轴平行![]() 直线
直线![]() 与x轴、y轴分别交于点E,
与x轴、y轴分别交于点E,![]() 将菱形ABCD沿x轴向左平移m个单位,当点D落在
将菱形ABCD沿x轴向左平移m个单位,当点D落在![]() 的内部时
的内部时![]() 不包括三角形的边
不包括三角形的边![]() ,m的值可能是
,m的值可能是![]()
![]()
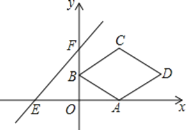
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
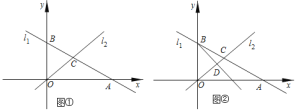
【题目】在平面直角坐标系中,直线![]() :
:![]() 分别与x轴、y轴交于点A、点B,且与直线
分别与x轴、y轴交于点A、点B,且与直线![]() :
:![]() 于点C.
于点C.
![]() Ⅰ
Ⅰ![]() 如图
如图![]() ,求出B、C两点的坐标;
,求出B、C两点的坐标;
![]() Ⅱ
Ⅱ![]() 若D是线段OC上的点,且
若D是线段OC上的点,且![]() 的面积为4,求直线BD的函数解析式.
的面积为4,求直线BD的函数解析式.
![]() Ⅲ
Ⅲ![]() 如图
如图![]() ,在
,在![]() Ⅱ
Ⅱ![]() 的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
的条件下,设P是射线BD上的点,在平面内是否存在点Q,使以O、B、P、Q为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y= ![]() x+1与抛物线y=ax2+bx﹣3交于A、B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A、B点重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.
x+1与抛物线y=ax2+bx﹣3交于A、B两点,点A在x轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A、B点重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.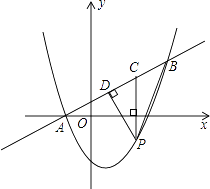
(1)求a、b及sin∠ACP的值;
(2)设点P的横坐标为m;
①用含有m的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积之比为9:10?若存在,直接写出m的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们把对角线相等的四边形叫做和美四边形.
![]() 请举出一种你所学过的特殊四边形中是和美四边形的例子.
请举出一种你所学过的特殊四边形中是和美四边形的例子.
![]() 如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
如图1,E,F,G,H分别是四边形ABCD的边AB,BC,CD,DA的中点,已知四边形EFGH是菱形,求证:四边形ABCD是和美四边形;
![]() 如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,
如图2,四边形ABCD是和美四边形,对角线AC,BD相交于O,![]() ,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.
,E、F分别是AD、BC的中点,请探索EF与AC之间的数量关系,并证明你的结论.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com