
分析 (1)分别将A,B,C点代入函数关系式进而判断即可;
(2)分别将P,Q点代入函数关系式进而得出答案.
解答 解:(1)当x=0时,y=2,
当x=2时,y=$\frac{8}{3}$+2=$\frac{14}{3}$,
当x=$\root{3}{9}$时,y=5,
故B,C点不在该函数图象上,A点在该函数图象上;
(2)当y=0时,0=$\frac{1}{3}$x3+2,
即0=$\frac{1}{3}$a3+2,
解得;a=$\root{3}{-6}$,
当x=-$\sqrt{3}$时,b=$\frac{1}{3}$×(-$\sqrt{3}$)3+2,
解得:b=2-$\sqrt{3}$.
点评 此题主要考查了函数关系式以及函数图象上点的坐标性质,正确理解图象上点的坐标性质是解题关键.


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:选择题
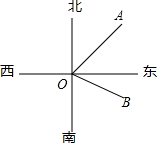 如图,在灯塔O处观测到轮船A位于东北方向,同时轮船B在南偏东55°方向,那么∠AOB的大小为( )
如图,在灯塔O处观测到轮船A位于东北方向,同时轮船B在南偏东55°方向,那么∠AOB的大小为( )| A. | 80° | B. | 90° | C. | 100° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,E为AC边的中点,过点A作AD⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF=∠CBG.求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com