
分析 分母是1的分数有1个,分母是2的分数由3个,分母是3的分数有5个,…分母是n的分数有2n-1个;分子都是从1开始到与分母的数字相同连续的自然数,再倒数回到1,由此规律解决问题:
(1)首先要计算第800个数之前最大的平方是:当n=28时,n2=784,第784个数是分母为28的最后一个数,
所以可以找到第800个数;
(2)先找分母是16的最后一个数是第162个数,162=256,再向右数5个即可,因为同一个分母的数除中间为1的数是一个外,其余都是2个,所以倒数第5个数也是$\frac{5}{17}$,得出结论;
(3)同(1)同理,先计算第552个数之前最大的平方数:当n=23时,n2=529,先计算分母为1至23的所有分数之和:1+2+3+…+23的值,再确定第529到552之间数的和,最后相加即可;
(4)因为分母为n的分数有2n-1个,且这2n-1个分数相加和为n.所以前分母为n的分数之和=$\frac{n(n+1)}{2}$,确定当n为最大时,最接近106时的n=14,即前196个数的和=$\frac{14×15}{2}$=105,与106还相差1,分母为15的分数能否达到几个分数和为1,来判断.
解答 解:观察数列$\frac{1}{1}$,$\frac{1}{2}$,$\frac{2}{2}$,$\frac{1}{2}$,$\frac{1}{3}$,$\frac{2}{3}$,$\frac{3}{3}$,$\frac{2}{3}$,$\frac{1}{3}$,$\frac{1}{4}$,…,
可发现:分母为1的分数有1个,分母为2的数有3个,分母为3的数有5个,
∴可得出:分母为n的分数有2n-1个,且这2n-1个分数相加和为n.
第12个是分母为1的最后一个,
第22个是分母为2的最后一个,
…
第n2个是分母n的最后一个
(1)∵1+3+5+…+2n-1=n2,
∴令n2≤800,
解得:n≤28,
当n=28时,n2=784,
∴第784个数是分母为28的最后一个数,
∴第800个数的分母为29,分子为800-784=16,
∴第800个数为$\frac{16}{29}$.
(2)∵162+5=256+5=261,
172-4=289-4=285,
∴$\frac{5}{17}$是第261个数或第285个数.
(3)令n2≤552,
解得:n≤23,
当n=23时,n2=529,
即前529个数的和=1+2+3+…+23=24×11+12=276,
第530至第552个数之间一共有:552-530+1=23个数,
第530至第552个数的和为:$\frac{1}{24}$+$\frac{2}{24}$+$\frac{3}{24}$+…+$\frac{23}{24}$=$\frac{276}{24}$=11.5,
∴前552个数的和是:276+11.5=287.5;
(4)分母为n时,前n2个数的和为:$\frac{n(n+1)}{2}$,
当n=14时,前142=196个数的和为:$\frac{14×15}{2}$=105,
第197个数开始为分母是15的数:$\frac{1}{15}$+$\frac{2}{15}$+$\frac{3}{15}$+$\frac{4}{15}$+$\frac{5}{15}$=1,
105+1=106,
所以存在前n个数的和等于106,此时n=196+5=201.
点评 此题考查数字的变化规律,难度较大,找出数字之间的联系,得出规律,解决问题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
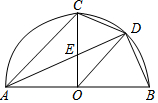 如图AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:
如图AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:| A. | ①②③ | B. | ①④⑤ | C. | ①③④ | D. | ①③④⑤ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,-2) | B. | (-3,2) | C. | (2,-3) | D. | (-2,-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ba | B. | 10b+a | C. | 10000b+a | D. | 100b+a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $-\frac{9}{2}$ | B. | $\frac{9}{2}$ | C. | 0 | D. | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 32,42,52 | B. | 1,$\sqrt{2}$,$\sqrt{3}$ | C. | 1,2,3 | D. | 12,22,32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com