
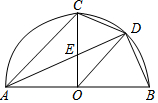
 如图AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:
如图AB是半圆直径,半径OC⊥AB于点O,AD平分∠CAB分别交OC于点E,交弧BC于点D,连结CD、OD,给出以下5个结论:| A. | ①②③ | B. | ①④⑤ | C. | ①③④ | D. | ①③④⑤ |
分析 ①根据等腰三角形的性质和角平分线的性质,利用等量代换求证∠CAD=∠ADO即可;
②过点O作OG⊥AC,再根据直角三角形斜边大于直角边可证;
③可证得△CED∽△CDO,根据相似三角形的对应边成比例,可得CD2=OC•CE=$\frac{1}{2}$AB•CE,即可证得结论;
④利用相似三角形的判定与性质以及等腰直角三角形的性质得出即可;
⑤△ADO和△DOE不相似,故线段OD不是DE与DA的比例中项.
解答 解:①∵AB是半圆直径,
∴AO=OD,
∴∠OAD=∠ADO,
∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAO=$\frac{1}{2}$∠CAB,
∴∠CAD=∠ADO,
∴AC∥OD,
∴故①正确.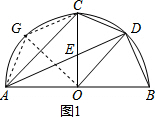 ②如图1,过点O作OG⊥AC,连接CG,AG,
②如图1,过点O作OG⊥AC,连接CG,AG,
∵OG⊥AC,
∴$\widehat{AG}$=$\widehat{CG}$,
∵半径OC⊥AB于点O,
∴$\widehat{AG}$=$\widehat{CG}$=$\widehat{CD}$,
∴AG=GC=CD,
∴AC<2CD,
∴故②错误.
③∵AB是半圆直径,
∴OC=OD,
∴∠OCD=∠ODC=67.5°,
∵∠CAD=∠ADO=22.5°,
∴∠CDE=∠ODC-∠ADO=67.5°-22.5°=45°,
∴△CED∽△CDO,
∴CD:OC=CE:CD,
∴CD2=OC•CE=$\frac{1}{2}$AB•CE,
∴2CD2=CE•AB.
故③正确.
④如图2,过点E作EM⊥AC于点M,
∵AO=CO,AO⊥CO,
∴∠CAO=∠ACO=45°,
∴CM=ME,
∵AD平分∠CAB分别交OC于点E,
EO⊥AO,EM⊥AC,
∴ME=EO,
∴CM=ME=EO,
∴CE=$\sqrt{2}$ME=$\sqrt{2}$EO,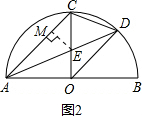
由①得:∵AC∥OD,
∴△ACE∽△DOE,
∴$\frac{EC}{EO}$=$\sqrt{2}$,
∴$\frac{{S}_{△AEC}}{{S}_{△DEO}}$=($\sqrt{2}$)2=2,
∴S△AEC=2S△DEO;
故④正确,
⑤∵AD平分∠CAB交弧BC于点D,
∴∠CAD=∠DAC=$\frac{1}{2}$×45°=22.5°,
∴∠COD=45°,
∵AC∥DO,
∴∠CAD=∠ADO=22.5°,
∴△ADO是等腰三角形,
△DOE中,∠ADO=22.5°,∠EOD=45°,
∴△ADO和△DOE不相似,
∴线段OD不是DE与DA的比例中项,
∴故⑤错误.
综上所述,只有①③④正确.
故选C.
点评 此题主要考查相似三角形的判定与性质,圆心角、弧、弦的关系,圆周角定理,等腰三角形的性质,三角形内角和定理等知识点的灵活运用,此题步骤繁琐,但相对而言,难易程度适中,很适合学生的训练是一道典型的题目.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| a/m | … | $\frac{1}{2}$ | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | … |
| cm 2 | … | … |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{\frac{1}{4}}$ | B. | $\sqrt{(-2)^{2}}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{-\frac{1}{4}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
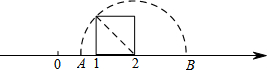 如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是( )
如图,以数轴的单位长度线段为边作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$-1 | C. | 2-$\sqrt{2}$ | D. | $\sqrt{2}$-$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是二次函数y=ax2+bx+c的图象,则下列判断正确的有( )
如图,是二次函数y=ax2+bx+c的图象,则下列判断正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com