
【题目】当m,n是正实数,且满足m+n=mn时,就称点P(m,![]() )为“完美点”.
)为“完美点”.
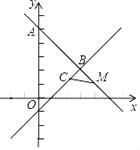
(1)若点E为完美点,且横坐标为2,则点E的纵坐标为 ;若点F为完美点,且横坐标为3,则点F的纵坐标为 ;
(2)完美点P在直线 (填直线解析式)上;
(3)如图,已知点A(0,5)与点M都在直线y=﹣x+5上,点B,C是“完美点”,且点B在直线AM上.若MC=![]() ,AM=4
,AM=4![]() ,求△MBC的面积.
,求△MBC的面积.
【答案】(1)1,2;(2)y=x﹣1;(3)△MBC的面积=![]() .
.
【解析】
(1)把m=2和3分别代入m+n=mn,求出n即可;
(2)求出两条直线的解析式,再把P点的坐标代入即可;
(3)由m+n=mn变式为![]() =m﹣1,可知P(m,m﹣1),所以在直线y=x﹣1上,点A(0,5)在直线y=﹣x+b上,求得直线AM:y=﹣x+5,进而求得B(3,2),根据直线平行的性质从而证得直线AM与直线y=x﹣1垂直,然后根据勾股定理求得BC的长,从而求得三角形的面积.
=m﹣1,可知P(m,m﹣1),所以在直线y=x﹣1上,点A(0,5)在直线y=﹣x+b上,求得直线AM:y=﹣x+5,进而求得B(3,2),根据直线平行的性质从而证得直线AM与直线y=x﹣1垂直,然后根据勾股定理求得BC的长,从而求得三角形的面积.
(1)把m=2代入m+n=mn得:2+n=2n,
解得:n=2,
即![]() =
=![]() =1,
=1,
所以E的纵坐标为1;
把m=3代入m+n=mn得:3+n=3n,
解得:n=![]() ,
,
即 ,
,
所以F的纵坐标为2;
故答案为:1,2;
(2)设直线AB的解析式为y=kx+b,
从图象可知:与x轴的交点坐标为(5,0)A(0,5),
代入得:![]() ,
,
解得:k=﹣1,b=5,
即直线AB的解析式是y=﹣x+5,
设直线BC的解析式为y=ax+c,
从图象可知:与y轴的交点坐标为(0,﹣1),与x轴的交点坐标为(1,0),
代入得:![]() ,
,
解得:a=1,c=﹣1,
即直线BC的解析式是y=x﹣1,
∵P(m,![]() ),m+n=mn且m,n是正实数,
),m+n=mn且m,n是正实数,
∴除以n得:![]() ,即
,即![]()
∴P(m,m﹣1)即“完美点”P在直线y=x﹣1上;
故答案为:y=x﹣1;
(3)∵直线AB的解析式为:y=﹣x+5,直线BC的解析式为y=x﹣1,
∴![]() ,
,
解得:![]() ,
,
∴B(3,2),
∵一、三象限的角平分线y=x垂直于二、四象限的角平分线y=﹣x,而直线y=x﹣1与直线y=x平行,直线y=﹣x+5与直线y=﹣x平行,
∴直线AM与直线y=x﹣1垂直,
∵点B是直线y=x﹣1与直线AM的交点,
∴垂足是点B,
∵点C是“完美点”,
∴点C在直线y=x﹣1上,
∴△MBC是直角三角形,
∵B(3,2),A(0,5),
∴![]()
∵![]() ,
,
∴![]()
又∵![]() ,
,
∴BC=1,
∴S△MBC=![]() .
.


科目:初中数学 来源: 题型:
【题目】已知如图,点 C 在以 AB 为直径的⊙O 上,点 D 在 AB 的延长线上,∠BCD =∠A.
(1)求证:CD 为⊙O 的切线;
(2)过点 C 作 CE⊥AB 于点 E.若 CE = 2,cos D =![]() ,求 AD 的长.
,求 AD 的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放x天后,将这批香菇一次性出售,设这批香菇的销售总金额为y元,试写出y与x之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额﹣收购成本﹣各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
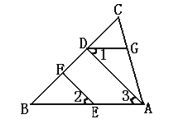
【题目】如图,EF∥AD,∠1=∠2,∠BAC=72 o,求∠AGD的度数.
解:因为EF∥AD
所以∠2= ( )
又因为∠1=∠2
所以∠1=∠3
所以AB∥ ( )
所以∠BAC+ =180 o( )
因为∠BAC=72 o
所以∠AGD= ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么这两次拐弯的角度是( )
A. 第一次向右拐40, 第二次向左拐140
B. 第一次向左拐40, 第二次向右拐40
C. 第一次向左拐40, 第二次向左拐140
D. 第一次向右拐40, 第二次向右拐40°
查看答案和解析>>
科目:初中数学 来源: 题型:
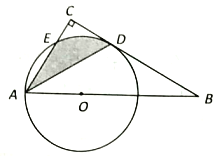
【题目】如图,点0 为Rt△ABC斜边AB上的一点,以OA 为半径的☉O与BC切于点D,与AC 交于点E,连接AD.
(1) 求证: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个形状、大小完全相同的含有30°、60°的直角三角板如图①放置,PA、PB与直线MN重合,且三角板PAC、三角板PBD均可绕点P逆时针旋转.
(1)直接写出∠DPC的度数.
(2)如图②,在图①基础上,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为5°/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为1°/秒,(当PA转到与PM重合时,两三角板都停止转动),在旋转过程中,当PC与PB重合时,求旋转的时间是多少?
(3)在(2)的条件下,PC、PB、PD三条射线中,当其中一条射线平分另两条射线的夹角时,请直接写出旋转的时间.

查看答案和解析>>
科目:初中数学 来源: 题型:
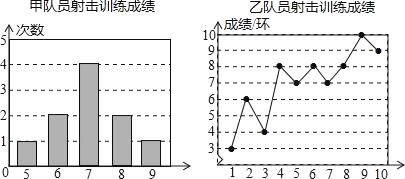
【题目】甲、乙两名队员参加射击训练(各射击10次),成绩分别被制成下列两个统计图:
根据以上信息,整理分析数据如下表:
平均成绩/环 | 中位数/环 | 众数/环 | 方差/环2 | |
甲 | a | 7 | 7 | 1.2 |
乙 | 7 | b | 8 | c |
(1)求出表格中a,b,c的值;
(2)分别运用表中的统计量,简要分析这两名队员的射击成绩,若选派其中一名参赛,你认为应选哪名队员?
查看答案和解析>>
科目:初中数学 来源: 题型:
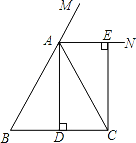
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com