
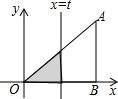
 如图所示,在直角△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分面积是S,则S与t之间的函数关系式是S=$\frac{1}{2}$t2(0≤t≤3).
如图所示,在直角△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分面积是S,则S与t之间的函数关系式是S=$\frac{1}{2}$t2(0≤t≤3). 分析 Rt△AOB中,AB⊥OB,且AB=OB=3,所以很容易求得∠AOB=∠A=45°;再由平行线的性质得出∠OCD=∠A,即∠AOD=∠OCD=45°,进而证明OD=CD=t;最后根据三角形的面积公式,解答出S与t之间的函数关系式.
解答 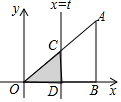 解:∵Rt△AOB中,AB⊥OB,且AB=OB=3,
解:∵Rt△AOB中,AB⊥OB,且AB=OB=3,
∴∠AOB=∠A=45°,
∵CD⊥OB,
∴CD∥AB,
∴∠OCD=∠A,
∴∠AOD=∠OCD=45°,
∴OD=CD=t,
∴S△OCD=$\frac{1}{2}$×OD×CD
=$\frac{1}{2}$t2(0≤t≤3),
∴S与t之间的函数关系式是S=$\frac{1}{2}$t2(0≤t≤3),
故答案为S=$\frac{1}{2}$t2(0≤t≤3).
点评 本题主要考查了动点问题的函数图象,根据题意列出函数关系式是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
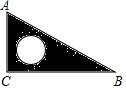 如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.
如图,一个直角三角形ABC的直角边BC=a,AC=b,三角形内部圆的半径为r.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
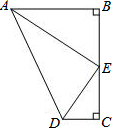 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠AEB;③S梯形ABCD=AD•CE;④AD=2AE,四个结论中成立的是( )
如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90°;②∠ADE=∠AEB;③S梯形ABCD=AD•CE;④AD=2AE,四个结论中成立的是( )| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com