

分析 (1)把B点和C点坐标分别代入y=$\frac{1}{2}$x2+bx+c得到关于b、c的方程组,然后解方程组求出b、c即可得到抛物线解析式;
(2)首先求出△PCE面积的表达式,然后利用二次函数的性质求出其最大值;
(3)易知D(-2,0),接着利用待定系数求出直线AC的解析式为y=-x-4,再根据直线PE与直线BC的解析式求得点E的坐标为(1,-2).求M点分类讨论:①当MD=OD时,求得M的坐标为(-2,-2);所以ME∥x轴,则∠PEM=45°,由翻折得∠NEM=90°,所以NE∥y轴,可得N(1,1);②当DM=OM时,求得M的坐标为(-1,-3),又可证得△MPE≌△BPE,所以N与B重合,N点坐标为(2,0);③OD=OM时,等腰△OMD不存在.
解答 解:(1)根据题意得:
$\left\{\begin{array}{l}{c=-4}\\{2+2b+c=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=1}\\{c=-4}\end{array}\right.$,
所以该抛物线的解析式为:y=$\frac{1}{2}$x2+x-4;
(2)令y=0,即$\frac{1}{2}$x2+x-4=0,解得x1=-4,x2=2,
∴A(-4,0),S△ABC=$\frac{1}{2}$AB•OC=12
设P点坐标为(x,0),则PB=2-x.
∵PE∥BC,
∴∠BPE=∠BAC,∠BEP=∠BCA,
∴△PBE∽△BAC,
∴$\frac{{S}_{△PBE}}{{S}_{△ABC}}$=($\frac{PB}{AB}$)2,即$\frac{{S}_{△PBE}}{12}$=($\frac{2-x}{6}$)2,
化简得:S△PBE=$\frac{1}{3}$(2-x)2.
S△PCE=S△PCB-S△PBE=$\frac{1}{2}$PB•OC-S△PBE=$\frac{1}{2}$×(2-x)×4-$\frac{1}{3}$(2-x)2
=-$\frac{1}{3}$x2-$\frac{2}{3}$x+$\frac{8}{3}$=-$\frac{1}{3}$(x+1)2+3
∴当x=-1时,S△PCE的最大值为3.
(3)由(2)已知A(-4,0),
∵点D为0A中点,
∴D(-2,0),
设直线AC的解析式为y=mx+n,
把A(-4,0)、C(0,-4)分别代入得:
$\left\{\begin{array}{l}{-4m+n=0}\\{n=-4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-1}\\{n=-4}\end{array}\right.$,
∴直线AC的解析式为y=-x-4.
∵PE∥AC,所以可设直线PE的解析式为y=-x+a,
将P(-1,0)代入y=-x-a得a=-1,
所以直线PE的解析式为y=-x-1.
设直线BC的解析式为y=kx+a′,
将B(2,0)、C(0,-4)代入y=kx+a′得$\left\{\begin{array}{l}{2k+a′=0}\\{a′=-4}\end{array}\right.$,
解得k=2,a′=-4.
所以直线BC的解析式为y=2x-4.
由2x-4=-x-1得x=1,将x=1代入y=2x-4得y=-2,
∴E点坐标为(1,-2).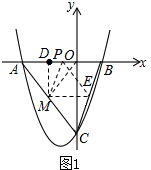 ①当MD=OD时,如图1:
①当MD=OD时,如图1:
∵AD=MD=AD,OA=OC,∠DAM=∠OAC,
∴△ADM∽△AOC,
∴∠ADM=∠AOC=90°,即DM⊥x轴,
∴M的横坐标为-2,将x=-2代入y=-x-4,得y=-2.
所以此时M的坐标为(-2,-2);
∵M和E点纵坐标相等,
∴ME∥x轴,
∴∠PEM=45°.
由翻折得∠ENM=2∠PEM=90°,即NE∥y轴,
∴EN=ME=3,
∵E(1,-2),
∴N(1,1).
②当DM=OM时,过点M作MG⊥x轴交于点,如图2: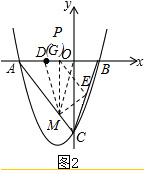
易知DG=OG=1,即G点与P点重合,M的横坐标为-1,
将x=-1代入y=-x-4,得y=-3.
∴M(-1,-3).
∵ME=$\sqrt{(-1-1)^{2}+(-3+2)^{2}}$=$\sqrt{5}$,EB=$\sqrt{(1-2)^{2}+{2}^{2}}$=$\sqrt{5}$,
∴ME=EB,
∵PB=3,PM=3,即PB=PM,
又∵PE=PE,
∴△BPE≌△MPE,
∴∠BEP=∠MEP,
∴点N与点B重合,
∴N(2,0);
③当OD=OM时,
设点O到AC的最短距离为h,则OA•OC=h•AC
∵AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,
∴h=$\frac{4×4}{4\sqrt{2}}$=2$\sqrt{2}$,
∵h>OD,
∴OD≠OM.此时等腰△OMD不存在.
综上所述,N点的坐标分别为(1,1)或(2,0).
点评 本题属于二次函数的综合应用.考查了待定系数法求一次函数与二次函数的解析式,等腰三角形的判定,图形翻折的性质,相似三角形的判定与性质等知识.具有一定的综合性与难度,解答本题时要注意方程思想、数形结合思想和分类讨论思想的应用.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
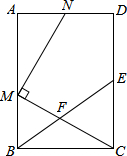 如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
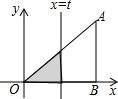 如图所示,在直角△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分面积是S,则S与t之间的函数关系式是S=$\frac{1}{2}$t2(0≤t≤3).
如图所示,在直角△AOB中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分面积是S,则S与t之间的函数关系式是S=$\frac{1}{2}$t2(0≤t≤3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com