
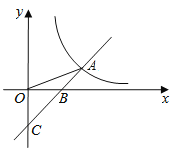
【题目】直线![]() 与
与![]() 轴交于点C,与
轴交于点C,与![]() 轴交于点B,与反比例函数
轴交于点B,与反比例函数![]() 的图象在第一象限交于点A,连接OA,若
的图象在第一象限交于点A,连接OA,若![]() ,则k的值为_____.
,则k的值为_____.
【答案】3
【解析】分析:先由直线y=x-2与y轴交于点C,与x轴交于点B,求出C(0,-2),B(2,0),由S△BOC=![]() OBOC,求出△BOC的面积,根据S△AOB:S△BOC=1:2,得出S△AOB的面积,求出yA=1,再把y=1代入y=x-2,解得x的值,得到A点坐标,然后将A点坐标代入y=
OBOC,求出△BOC的面积,根据S△AOB:S△BOC=1:2,得出S△AOB的面积,求出yA=1,再把y=1代入y=x-2,解得x的值,得到A点坐标,然后将A点坐标代入y=![]() ,即可求出k的值.
,即可求出k的值.
详解:∵直线y=x-2与y轴交于点C,与x轴交于点B,
∴C(0,-2),B(2,0),
∴S△BOC=![]() OBOC=
OBOC=![]() ×2×2=2,
×2×2=2,
∵S△AOB:S△BOC=1:2,
∴S△AOB=![]() S△BOC=1,
S△BOC=1,
∴![]() ×2×yA=1,
×2×yA=1,
∴yA=1,
把y=1代入y=x-2,
得1=x-2,解得x=3,
∴A(3,1).
∵反比例函数y=![]() 的图象过点A,
的图象过点A,
∴k=3×1=3.
故答案为:3.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】某商场第一次用11000元购进某款拼装机器人进行销售,很快销售一空,商家又用24000元第二次购进同款机器人,所购进数量是第一次的2倍,但单价贵了10元.
(1)求该商家第一次购进机器人多少个?
(2)若所有机器人都按相同的标价销售,要求全部销售完毕的利润率不低于20%(不考虑其它因素),那么每个机器人的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号电视机的方案中,为使销售利润最多,你选择哪一种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划购买A、B两种计算器共100个,要求A种计算器数量不低于B种的![]() ,且不高于B种的
,且不高于B种的![]() .已知A、B两种计算器的单价分别是150元/个、100元/个,设购买A种计算器x个.
.已知A、B两种计算器的单价分别是150元/个、100元/个,设购买A种计算器x个.
(1)求计划购买这两种计算器所需费用y(元)与x的函数关系式;
(2)问该公司按计划购买者两种计算器有多少种方案?
(3)由于市场行情波动,实际购买时,A种计算器单价下调了3m(m>0)元/个,同时B种计算器单价上调了2m元/个,此时购买这两种计算器所需最少费用为12150元,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数轴上,点A、B分别表示有理数a、b,则 |a-b| 可以表示点A、B之间的距离,如|a-2| =1表示到点2的距离等于1的点,a=3或1.
按照要求在数轴上标出点A的位置,并写出a的值.
(1)若 |a-0| =3,则a=________;
![]()
(2)若 |a-1| =3,则a=_______;
![]()
(3)若 |a+1| =3,则a=__________;
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场统计了今年1~5月A,B两种品牌冰箱的销售情况,并将获得的数据绘制成折线统计图
(1)该商场这段时间内A.B两种品牌冰箱月销售量的中位数分别为 , ;
(2)计算两种品牌月销售量的方差,比较并说明该商场1~5月这两种品牌冰箱月销售量的稳定性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某校文学社团随机调查了部分学生,就“你最喜欢的图书类别”(只选一项)对学生课外阅读的情况作了调查统计,将调查结果统计后绘制成如下统计表和条形统计图.请根据统计图表提供的信息解答下列问题:
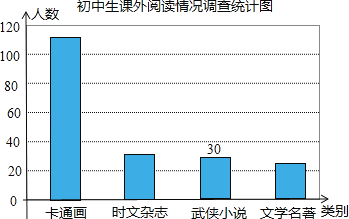
初中生课外阅读情况调查统计表
种类 | 频数 | 频率 |
卡通画 | a | 0.56 |
时文杂志 | 32 | b |
武侠小说 | c | 0.15 |
文学名著 | 26 | d |
(1)这次随机调查了几名学生?统计表中a,d各代表什么数值?
(2)试估计该校1500名学生中有多少名同学最喜欢文学名著类书籍?
(3)结合以上统计数据,请你站在文学社团的立场发表一下你的看法.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com