
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
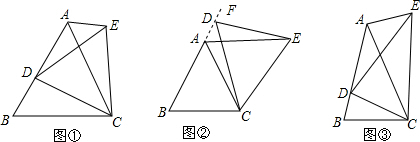
 若已知两点之间的所有连线中,线段最短,那么你能否试着解决下面的问题呢?
若已知两点之间的所有连线中,线段最短,那么你能否试着解决下面的问题呢?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC与点E,PF⊥CD于点F,连接EF,给出的下列结论:①AP=EF;②∠PFE=∠BAP;③PD=EC;④PB2+PD2=2PA2,正确的个数有( )
如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC与点E,PF⊥CD于点F,连接EF,给出的下列结论:①AP=EF;②∠PFE=∠BAP;③PD=EC;④PB2+PD2=2PA2,正确的个数有( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小鹏的手中有一根长为40cm的铜丝,他想用这根铜丝分段围成一个面积为50cm2的如图所示的“日“字的矩形钢丝框,求该矩形钢丝框的长.设该矩形铜丝框的长为xcm,根据题意,可列方程为( )
小鹏的手中有一根长为40cm的铜丝,他想用这根铜丝分段围成一个面积为50cm2的如图所示的“日“字的矩形钢丝框,求该矩形钢丝框的长.设该矩形铜丝框的长为xcm,根据题意,可列方程为( )| A. | x($\frac{40-3x}{2}$)=50 | B. | x($\frac{40-2x}{3}$)=50 | C. | x(40-3x)=50 | D. | x(40-2x)=50 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
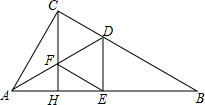 如图,△ABC中,∠ACB=90°,AD是∠CAB的平分线,交BC于D,CH是AB边上的高,交AD于F,DE⊥AB于E,求证:四边形CDEF是菱形.
如图,△ABC中,∠ACB=90°,AD是∠CAB的平分线,交BC于D,CH是AB边上的高,交AD于F,DE⊥AB于E,求证:四边形CDEF是菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com