
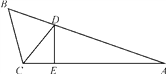
【题目】如图,在△ABC中,∠A=20°,CD是∠BCA的平分线,△CDA中,DE是CA边上的高,又有∠EDA=∠CDB,求∠B的大小.
【答案】∠B=60°.
【解析】试题分析:∠A=20°,DE是CA边上的高,所以∠EDA=∠CDB=90°-20°=70°,根据外角的性质得∠CDB=∠A+∠DCE=70°,所以∠DCE=∠BCD=50°,所以∠B=180°-∠BCD-∠CDB=60°.
∵DE是CA边上的高,
∴∠DEA=∠DEC=90°.
∵∠A=20°,
∴∠EDA=90°-20°=70°.
∵∠EDA=∠CDB,
∴∠CDE=180°-70°×2=40°.
在Rt△CDE中,∠DCE=90°-40°=50°.
∵CD是∠BCA的平分线,
∴∠BCA=2∠DCE=2×50°=100°.
∴∠B=180°-∠BCA-∠A=60°.


科目:初中数学 来源: 题型:
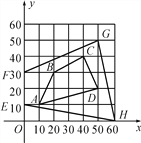
【题目】长阳公园有四棵古树A,B,C,D (单位:米).
(1)请写出A,B,C,D四点的坐标;
(2)为了更好地保护古树,公园决定将如图所示的四边形EFGH用围栏圈起来,划为保护区,请你计算保护区的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
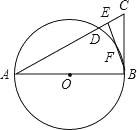
【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠EBC=![]() ∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
∠BAC,以AB为直径的⊙O交AC于点D,交EB于点F.
(1)求证:BC与⊙O相切;
(2)若AB=8,sin∠EBC=![]() ,求AC的长.
,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com