Question

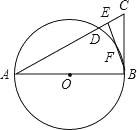
【题目】如图，△ABC中，E是AC上一点，且AE=AB，∠EBC=∠BAC，以AB为直径的⊙O交AC于点D，交EB于点F．

（1）求证：BC与⊙O相切；

（2）若AB=8，sin∠EBC=，求AC的长．

Answer 1

【答案】（1）证明见解析（2）

【解析】

试题分析：（1）首先连接AF，由AB为直径，根据圆周角定理，可得∠AFB=90°，又由AE=AB，∠EBC=∠BAC，根据等腰三角形的性质，可得∠BAF=∠EBC，继而证得BC与⊙O相切；

（2）首先过E作EG⊥BC于点G，由三角函数的性质，可求得BF的长，易证得△CEG∽△CAB，然后由相似三角形的对应边成比例，求得答案．

试题解析：（1）连接AF．

∵AB为直径，

∴∠AFB=90°．

∵AE=AB，

∴△ABE为等腰三角形．

∴∠BAF=∠BAC．

∵∠EBC=∠BAC，

∴∠BAF=∠EBC，

∴∠FAB+∠FBA=∠EBC+∠FBA=90°．

∴∠ABC=90°．

即AB⊥BC，

∴BC与⊙O相切．

（2）过E作EG⊥BC于点G，

∵∠BAF=∠EBC，

∴sin∠BAF=sin∠EBC=．

在△AFB中，∠AFB=90°，

∵AB=8，

∴BF=ABsin∠BAF=8×=2，

∴BE=2BF=4．

在△EGB中，∠EGB=90°，

∴EG=BEsin∠EBC=4×=1，

∵EG⊥BC，AB⊥BC，

∴EG∥AB，

∴△CEG∽△CAB，

∴ ．

∴ ，

∴CE=，

∴AC=AE+CE=8+=．