
【题目】如图,在△ABC中,∠C=90°,∠A>∠B.
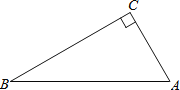
(1)用直尺和圆规作AB的垂直平分线,交AB与D,交BC于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若CE=DE,求∠A,∠B的度数.
【答案】(1)见解析;(2)∠B=30°,∠BAC=60°.
【解析】
试题分析:(1)利用基本作图(作线段的垂直平分线)作出DE;
(2)先利用角平分线性质定理的逆定理得到AE平分∠DAC,即∠CAE=∠BAE,再根据线段垂直平分线的性质定理得到EA=EB,则∠B=∠BAE,所以∠BAC=2∠B,再利用互余得到∠B+∠BAC=90°,于是得到∠B=30°,∠BAC=60°.
解:(1)如图,DE为所作;
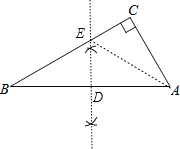
(2)连结AE,如图,
∵EC⊥AC,ED⊥AD,CE=DE,
∴AE平分∠DAC,即∠CAE=∠BAE,
∵ED垂直平分AB,
∴EA=EB,
∴∠B=∠BAE,
∴∠BAC=2∠B,
∵∠B+∠BAC=90°,
∴∠B=30°,∠BAC=60°.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠BOE=90°,OM平分∠AOD,ON平分∠DOE.
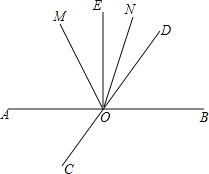
(1)若∠EON=18°,求∠AOC的度数.
(2)试判断∠MON与∠AOE的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为( )cm2.

A.8 B.9 C.10 D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了审核书稿中的错别字,选择抽样调查
B.为了了解春节联欢晚会的收视率,选择全面调查
C.“射击运动员射击一次,命中靶心”是随机事件
D.“经过由交通信号灯的路口,遇到红灯”是必然事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个形状、大小完全相同的含有30゜、60゜的三角板如图①放置,PA、PB与直线MN重合,且三角板PAC,三角板PBD均可以绕点P逆时针旋转.
(1)直接写出∠DPC的度数.
(2)若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定角度(如图②),若PF平分∠APD,PE平分∠CPD,求∠EPF的度数;
(3)如图③,在图①基础上,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3゜/秒,同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2゜/秒,(当PC转到与PM重合时,两三角板都停止转动),在旋转过程中,当2∠CPD=3∠BPM,求旋转的时间是多少.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,已知ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )
A.(﹣2,1) B.(﹣2,﹣1) C.(﹣1,﹣2) D.(﹣1,2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com