
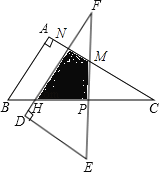
【题目】如图,△ABC中,∠A=90°,∠C=30°,BC=12cm,把△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,DF交BC于点H.△ABC与△DEF重叠部分的面积为( )cm2.

A.8 B.9 C.10 D.12
【答案】B
【解析】
试题分析:如图,由点P为斜边BC的中点得到PC=![]() BC=6,再根据旋转的性质得PF=PC=6,∠FPC=90°,∠F=∠C=30°,根据含30度的直角三角形三边的关系,在Rt△PFH中计算出PH=
BC=6,再根据旋转的性质得PF=PC=6,∠FPC=90°,∠F=∠C=30°,根据含30度的直角三角形三边的关系,在Rt△PFH中计算出PH=![]() PF=2
PF=2![]() ;在Rt△CPM中计算出PM=
;在Rt△CPM中计算出PM=![]() PC=2
PC=2![]() ,且∠PMC=60°,则∠FMN=∠PMC=60°,于是有∠FNM=90°,FM=PF﹣PM=6﹣2
,且∠PMC=60°,则∠FMN=∠PMC=60°,于是有∠FNM=90°,FM=PF﹣PM=6﹣2![]() ,则在Rt△FMN中可计算出MN=
,则在Rt△FMN中可计算出MN=![]() FM=3﹣
FM=3﹣![]() ,FN=
,FN=![]() MN=3
MN=3![]() ﹣3,然后根据三角形面积公式和利用△ABC与△DEF重叠部分的面积=S△FPH﹣S△FMN进行计算即可.
﹣3,然后根据三角形面积公式和利用△ABC与△DEF重叠部分的面积=S△FPH﹣S△FMN进行计算即可.
解:如图,
∵点P为斜边BC的中点,
∴PB=PC=![]() BC=6,
BC=6,
∵△ABC绕着它的斜边中点P逆时针旋转90°至△DEF的位置,
∴PF=PC=6,∠FPC=90°,∠F=∠C=30°,
在Rt△PFH中,∵∠F=30°,
∴PH=![]() PF=
PF=![]() ×6=2
×6=2![]() ,
,
在Rt△CPM中,∵∠C=30°,
∴PM=![]() PC=
PC=![]() ×6=2
×6=2![]() ,∠PMC=60°,
,∠PMC=60°,
∴∠FMN=∠PMC=60°,
∴∠FNM=90°,
而FM=PF﹣PM=6﹣2![]() ,
,
在Rt△FMN中,∵∠F=30°,
∴MN=![]() FM=3﹣
FM=3﹣![]() ,
,
∴FN=![]() MN=3
MN=3![]() ﹣3,
﹣3,
∴△ABC与△DEF重叠部分的面积=S△FPH﹣S△FMN
=![]() ×6×2
×6×2![]() ﹣
﹣![]() (3﹣
(3﹣![]() )(3
)(3![]() ﹣3)
﹣3)
=9(cm2).
故选:B.


科目:初中数学 来源: 题型:
【题目】同时抛掷两枚质地均匀的正方体骰子(骰子每一面的点数分别是从1到6这六个数字中的一个),以下说法正确的是( )
A. 掷出两个1点是不可能事件 B. 掷出两个骰子的点数和为6是必然事件
C. 掷出两个6点是随机事件 D. 掷出两个骰子的点数和为14是随机事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列语句中正确的个数为______.
(1)延长射线OA到点B;
(2)直线AB比射线CD长;
(3)线段AB就是A、B两点间的距离;
(4)角的大小与角两边的长度无关.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段CD在线段AB上,且CD=2,若线段AB的长度是一个正整数,则图中以A,B,C,D这四点中任意两点为端点的所有线段长度之和可能是( )
![]()
A.28 B.29 C.30 D.31
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠A>∠B.
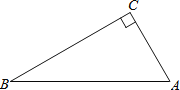
(1)用直尺和圆规作AB的垂直平分线,交AB与D,交BC于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,若CE=DE,求∠A,∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列条件不能判断△ABC是直角三角形的是( )
A. ∠B=50° ,∠C=40° B. ∠B=∠C=45
C. ∠A,∠B,∠C的度数比为5:3:2 D. ∠A-∠B=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在⊙O的直径AB的延长线上,点C在⊙O上,AC=CD,∠ACD=120°.
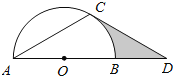
(1)求证:CD是⊙O的切线;
(2)若⊙O的半径为2,求图中阴影部分的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com