
����Ŀ����ͼ��������״����С��ȫ��ͬ�ĺ���30�b��60�b�����ǰ���ͼ�ٷ��ã�PA��PB��ֱ��MN�غϣ������ǰ�PAC�����ǰ�PBD�������Ƶ�P��ʱ����ת��
��1��ֱ��д����DPC�Ķ�����
��2�������ǰ�PAC�ı�PA��PN����ʼ�Ƶ�P��ʱ����תһ���Ƕȣ���ͼ�ڣ�����PFƽ����APD��PEƽ����CPD������EPF�Ķ�����
��3����ͼ�ۣ���ͼ�ٻ����ϣ������ǰ�PAC�ı�PA��PN����ʼ�Ƶ�P��ʱ����ת��ת��Ϊ3�b/�룬ͬʱ���ǰ�PBD�ı�PB��PM����ʼ�Ƶ�P��ʱ����ת��ת��Ϊ2�b/�룬����PCת����PM�غ�ʱ�������ǰ嶼ֹͣת����������ת�����У���2��CPD=3��BPM������ת��ʱ���Ƕ��٣�

���𰸡���1��90�b����2��30�b��3��22.5�룮
��������
�����������1�����ú���30�b��60�b�����ǰ�ó���DPC=180������CPA����DPB������������ɣ�
��2������CPE=��DPE=x����CPF=y������APF=��DPF=2x+y������������CPA=60�b������ɣ�
��3������תʱ��Ϊt�룬����BPM=2t�㣬��CPD=90����t�㣬�õ�2��90��t��=3��2t�����ɽ��
�⣺��1���ߡ�DPC=180������CPA����DPB����CPA=60������DPB=30����
���DPC=180�b��30�b��60�b=90�b��
��2������CPE=��DPE=x����CPF=y��
����APF=��DPF=2x+y��
�ߡ�CPA=60�b��
��y+2x+y=60�b��
��x+y=30�b
���EPF=x+y=30�b
��3������תʱ��Ϊt�룬���У�
��BPM=2t������CPD=180����30�㩁60�㩁3t��+2t��=90�㩁t��
��2��90��t��=3��2t
��t=22.5 ����2��CPD=3��BPM����ת��ʱ��Ϊ22.5�룮


 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ǽס�������˾���������������������ͳ��ͼ������ͳ��ͼ�ó����н��ۣ�������ȷ���ǣ� ��

A����˾������������������ٶȱ��ҹ�˾��
B���ҹ�˾������������������ٶȱȼ�˾��
C���ס�������˾������������������ٶ�һ����
D������ȷ���ס�������˾�����������������ٶȵĿ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C=90������A����B��
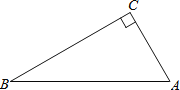
��1����ֱ�ߺ�Բ����AB�Ĵ�ֱƽ���ߣ���AB��D����BC��E������д������������ͼ�ۼ���
��2���ڣ�1���������£���CE=DE������A����B�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������4��8��4��6��3��������ƽ�����ֱ��ǣ� ��
A��5��4 B��8��5 C��6��5 D��4��5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������и����߶γ�Ϊ�ߣ�����������ε��ǣ� ��
A. 1 cm��2 cm��4 cm B. 8 cm��6 cm,4 cm
C. 12 cm��5 cm��6 cm D. 2 cm��3 cm ,5 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x�ֱ�ȡ��![]() ����
����![]() ����
����![]() ��������
��������![]() ����2����1��0��1��2������2015��2016��2017ʱ�������ʽ
����2����1��0��1��2������2015��2016��2017ʱ�������ʽ![]() ��ֵ���ٽ����ý����ӣ���͵��� ��
��ֵ���ٽ����ý����ӣ���͵��� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������ᣬ�����������⣺
��1���������ͼ��A��B�����λ�ã��ֱ�д����������ʾ����������
��2������A��B����֮��ľ����Ƕ��٣�
��3���������ϻ������A�ľ���Ϊ2�ĵ㣨�ò�ͬ��A��B��������ĸ��ʾ������д����Щ���ʾ������
![]()
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com